Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Ta có:
+) u23 + u57 = 29 ⇔ u1 + 22d + u1 + 56d = 29 ⇔ 2 u1 + 78d = 29
+) 3 u1 + u10 + u70 + u157 = 3 u1 + u1 + 9d + u1 + 69d + u1 + 156d = 6 u1 + 234d
= 3(2 u1 + 78d) = 3.29 = 87

Chọn C.
Có: u4 + u8 + u12 + u16 = 224 ⇔ u1 + 3d + u1 + 7d + u1 + 15d = 224
⇔ 4 u1 + 36d = 224 ⇔ u1 + 9d = 56
Ta có: S19 = 19/2. (2 u1 + 18d) = 19(u1 + 9d) = 19.56 = 1064

\(\left\{{}\begin{matrix}u_1+d=3\\u_1+9d=-15\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=\dfrac{21}{4}\\d=-\dfrac{9}{4}\end{matrix}\right.\)
\(S_{20}=\dfrac{21}{4}.20+\dfrac{19.20}{2}.\left(-\dfrac{9}{4}\right)=-\dfrac{645}{2}\)

Chọn đáp án D
Sử dụng công thức:
Cho cấp số cộng có số hạng đầu u 1 và công sai d thì số hạng thứ n ( n > 1 )
là u n = u 1 + ( n - 1 ) d
Từ đó ta tìm được công sai d
Cách giải
Ta có u 10 = u 1 + 9 d ⇔ 9 d = 27 ⇔ d = 3

Bài 4:
\(u_n=5.\left(\frac{1}{2}\right)^{2n-1}=10.\left(\frac{1}{2}\right)^{2n}=10\left(\frac{1}{4}\right)^n\)
Là cấp số nhân với \(u_1=10\) và công bội \(q=\frac{1}{4}\)
Bài 5:
\(S_5=u_1.\frac{q^4-1}{q-1}=u_1.\frac{\left(\frac{1}{3}\right)^4-1}{\frac{1}{3}-1}=\frac{121}{81}u_1\)
\(\Rightarrow u_1=\frac{81}{121}S_5=81\)
Bài 6:
\(\left\{{}\begin{matrix}u_1q=4\\u_1q^3=9\end{matrix}\right.\) \(\Rightarrow\left(u_1q^2\right)^2=36\Rightarrow\left[{}\begin{matrix}u_1q^2=6\\u_1q^2=-6\end{matrix}\right.\)
Mà \(u_3=u_1q^2\Rightarrow u_3=\pm6\)
Bài 2:
\(\left\{{}\begin{matrix}u_1q^3-u_1q=24\\u_1q^2-u_1=12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1q\left(q^2-1\right)=24\\u_1\left(q^2-1\right)=12\end{matrix}\right.\)
\(\Leftrightarrow\frac{u_1q\left(q^2-1\right)}{u_1\left(q^2-1\right)}=\frac{24}{12}\Rightarrow q=2\Rightarrow u_1=\frac{12}{q^2-1}=4\)
\(\Rightarrow S_8=u_1.\frac{q^8-1}{q-1}=4\left(2^8-1\right)=...\)
Câu 3:
\(u_{10}=u_1q^9=4\left(-2\right)^9=-2^{11}\)
\(S_{15}=u_1.\frac{q^{15}-1}{q-1}=4.\frac{\left(-2\right)^{15}-1}{-3}=\frac{3}{4}\left(2^{15}+1\right)\)
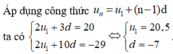
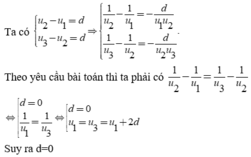
Chọn C.
Ta có: u23 + u57 = 29 ⇔ u1 + 22d + u1 + 56d = 29 ⇔ 2u1 + 78d = 29
Ta có: 3u1 + u10 + u70 + u157 = 3u1 + u1 +9d + u1 + 69d + u1 + 156d
= 6u1 + 234d = 3(2u1 + 78d) = 3.29 = 87