Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(AB=\sqrt{BC^2-AC^2}=6\left(cm\right)\)
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
Do đó: ΔCAB=ΔCAD

a: BC=căn 5^2+12^2=13cm
b: AB<AC<BC
=>góc C<góc B<góc A
c: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
=>ΔCAB=ΔCAD
d: góc EAC=góc ACB
góc ACB=góc ECA
=>góc EAC=góc ECA
=>ΔEAC cân tại E

a)
Xét △ABC vuông tại A có :
BC2=AB2+AC2(định lý py-ta-go)
⇒102=62+AC2
⇒100=36+AC2
⇒AC2=100-36=64
⇒AC=8cm
Xét △ABC có AC>AB(8>6)
⇒∠B>∠C(quan hệ giữa góc và cạnh đối diện)

a: BC=8cm
BC>AC
=>góc A>góc B
b: XétΔABD có
AC vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
c: GB+2GC=GB+GA>AB

Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng

`@` `\text {dnv4510}`
`a,`
Xét `\Delta ABC:`
`\text {BC > AC > AB (5 cm > 4 cm > 3 cm)}`
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`=>` $\widehat {A} > \widehat {B} > \widehat {C}$.
`b,`
Ta có: A là trung điểm của BD
`-> \text {AC là đường trung tuyến}` `(1)`
K là trung điểm của BC
`-> \text {DK là đường trung tuyến}` `(2)`
Mà \(\text{AC }\cap\text{ DK = M}\) `(3)`
Từ `(1), (2)` và `(3)`
`-> \text {M là trọng tâm của} \Delta ABC`
`@` Theo tính chất của trọng tâm trong `\Delta`
\(\text{MC = }\dfrac{2}{3}\text{AC}\)
Mà \(\text{AC = 4 cm}\)
`->`\(\text{MC = }\dfrac{2}{3}\cdot4=\dfrac{8}{3}\left(\text{cm}\right)\)
Vậy, độ dài của MC là `8/3 cm`
`b,`
Ta có: \(\left\{{}\begin{matrix}\text{A là trung điểm của BC}\\\text{AC }\bot\text{ BD}\end{matrix}\right.\)
`->`\(\text{CA là đường trung trực}\)
Ta có: \(\left\{{}\begin{matrix}\text{AC là đường trung trực (hạ từ đỉnh A)}\\\text{AC là đường trung tuyến (hạ từ đỉnh A) }\end{matrix}\right.\)
`@` Theo tính chất của các đường trong `\Delta` với `\Delta` cân
`->` \(\Delta\text{ BDC cân tại C (đpcm).}\)
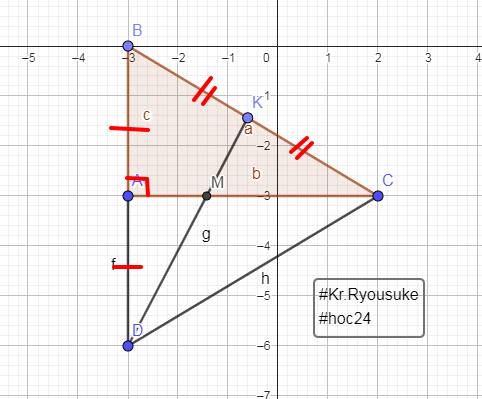
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔCBD có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3CA=8/3cm
c: Xét ΔCBD co
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C
a).
Áp dụng đl pytago vào tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2=3^2+4^2\Rightarrow BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
So sánh góc:
\(\widehat{C}< \widehat{B}< \widehat{A}\)
b) . Xét 2 t/g vuông : ABC và ADC có :
\(\widehat{CAB}=\widehat{CAD}=90^o\)
AC cạnh chung
\(AB=AD\left(theođề\right)\)
do đó : t/g ABC = t/g ADC ( cạnh góc vuông - cạnh góc vuông).
c) . Vì t/g ABC = t/g ADC
=> \(\widehat{BCA}=\widehat{DCA}\left(1\right)\)
Vì AM // BC
= > \(\widehat{CAM}=\widehat{BCA}\left(soletrong\right)\left(2\right)\)
Từ (1) và (2)
=> \(\widehat{DCA}=\widehat{CAM}\) ( 2 góc đều = góc BCA ) .
=> tam giác AMC cân ( 2 góc đáy bằng nhau).
d) . Từ đề ta suy ra :
G là trực tâm của t/g CBD
=> \(CG=\dfrac{2}{3}AC=\dfrac{2}{3}.4=2,67\left(cm\right)\)