Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét hai tam giác vuông ABC và tam giác vuông ADC có:
Cạnh AC chung
BA = DA
\(\Rightarrow\Delta ABC=\Delta ADC\) (Hai cạnh góc vuông)
\(\Rightarrow BC=DC\)
Hay tam giác BCD cân tại C.
b) Xét tam giác BKN và tam giác CDN có:
BN = CN
\(\widehat{BNK}=\widehat{CND}\) (Đối đỉnh)
\(\widehat{KBN}=\widehat{DCN}\) (So le trong)
\(\Rightarrow\Delta BKN=\Delta CDN\left(g-c-g\right)\)
\(\Rightarrow DN=KN\)
c) Do AM // BC nên \(\widehat{MAC}=\widehat{BCA}\)
Mà \(\widehat{BCA}=\widehat{ACM}\) nên \(\widehat{MAC}=\widehat{MCA}\Rightarrow MA=MC\)
Từ đó ta cũng có \(\widehat{DAM}=\widehat{MDA}\Rightarrow MD=MA\)
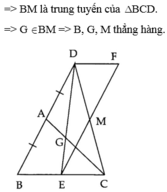
Vậy nên MD = MC hay M là trung điểm DC
Xét tam giác DBC có DN, CA, BM là các đường trung tuyến nên chúng đồng quy tại một điểm.
Lại có AC giao N tại O nên O thuộc BM hay B, M, O thẳng hàng.
Bài giải :

a) Xét hai tam giác vuông ABC và tam giác vuông ADC có:
Cạnh AC chung
BA = DA
⇒ΔABC=ΔADC (Hai cạnh góc vuông)
⇒BC=DC
Hay tam giác BCD cân tại C.
b) Xét tam giác BKN và tam giác CDN có:
BN = CN
^BNK=^CND (Đối đỉnh)
^KBN=^DCN (So le trong)
⇒ΔBKN=ΔCDN(g−c−g)
⇒DN=KN
c) Do AM // BC nên ^MAC=^BCA
Mà ^BCA=^ACM nên ^MAC=^MCA⇒MA=MC
Từ đó ta cũng có ^DAM=^MDA⇒MD=MA
Vậy nên MD = MC hay M là trung điểm DC
Xét tam giác DBC có DN, CA, BM là các đường trung tuyến nên chúng đồng quy tại một điểm.
Lại có AC giao N tại O nên O thuộc BM hay B, M, O thẳng hàng.

cho tam giác ABC vuông tại A, trên tia đối của tia AB lấy điểm D sao cho AB=AD.
a) C/m: Tam giác ABC=tam giác ADC
b)Biết AC=8cm, BC=10cm. So sánh các góc của tam giác ABC
c)Gọi N là trung điểm của BC, đường thẳng qua B song song với CD cắt DN tại K. C/m: DN=NK. Từ dó =>2DN<DC+DB
d)Đường thẳng qua A song song với BC cắt CD tại M. C/m: M là trung điểm của CD.

a) Xét \(\Delta\)ABC vuông tại A và \(\Delta\)ADC vuông tại A có:
AC là cạnh chung
AB = AD (gt)
\(\Rightarrow\)\(\Delta\)ABC = \(\Delta\)ADC (2cgv)
\(\Rightarrow\) BC = CD (2 cạnh tương ứng)
\(\Rightarrow\) \(\Delta\)BCD cân tại C (dhnb)
b) Vì BK // CD(gt)
\(\Rightarrow\) \(\widehat{KBC}=\widehat{BCD}\left(slt\right)\)
Hay \(\widehat{KBN}=\widehat{NCD}\)
Xét \(\Delta\)BNK và \(\Delta\)CND có:
\(\widehat{KBN}=\widehat{NCD}\) (cmt)
BN = CN (N là trung điểm của BC)
\(\widehat{BNK}=\widehat{CND}\)(đối đỉnh)
\(\Rightarrow\) \(\Delta\)BNK = \(\Delta\)CND (g - c - g)
\(\Rightarrow\) NK = ND
Mashiro ShiinaPhạm Nguyễn Tất ĐạtNhã DoanhNeettthNguyễn Thanh HằngKien NguyenĐời về cơ bản là buồn... cười!!!Trần Đăng NhấtHung nguyenNguyễn Huy TúNguyễn Huy ThắngAkai Harumasoyeon_Tiểubàng giảiNguyễn Thanh HằngPhương AnMashiro ShiinaVõ Đông Anh Tuấn

a: Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
Do đó;ΔCBD cân tại C
b: Xét ΔDNC và ΔKNB có
\(\widehat{DNC}=\widehat{KNB}\)
NC=NB
góc NCD=góc NBK
Do đo: ΔDNC=ΔKNB
Suy ra: DN=KN
c: Xét ΔABC có
A là trung điểm của BD
AM//CB
Do đó: M là trung điểmcủa CD
Xét ΔCDB có
CA là đường trung tuyến
DNlà đường trung tuyến
CA cắt DN tại O
Do đó: O là trọng tâm
=>B,M,O thẳng hàng