Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Thay giá trị x = -1 vào đa thức, ta có:
a(-1)2 + b(-1) + c = a – b + c
Vậy giá trị đa thức bằng a – b + c tại x = -1
* Thay giá trị x = 1 vào đa thức, ta có:
a.12 + b.1 + c = a + b + c
Vậy giá trị đa thức bằng a + b + c tại x = 1.

b) Thay x=-1; y=1 và z=-2 vào B, ta được:
\(B=\dfrac{3\cdot\left(-1\right)\cdot1\cdot\left(-2\right)-2\cdot\left(-2\right)^2}{\left(-1\right)^2+1}=\dfrac{6-8}{1+1}=\dfrac{-2}{2}=-1\)

Bài làm
Thay x = 1, y = -1 vào đa thức B. Ta được:
B = a.12.(-1)2 - b.14.(-1) + c.1.(-1)6
B = a . 1 . 1 - b . 1 . ( -1) + c . 1 . 1
B = a - ( - b ) + c
B = a + b + c
Mà a + b + c = 2019
=> B = a + b + c
Hay B = 2019
Vậy B = 2019
# Chúc bạn học tốt #

\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) ⇒ \(\dfrac{x^2}{a^2}=\dfrac{y^2}{b^2}=\dfrac{z^2}{c^2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x^2}{a^2}\) = \(\dfrac{y^2}{b^2}\) = \(\dfrac{z^2}{c^2}\) = \(\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}\) = \(\dfrac{x^2+y^2+z^2}{1}\) = \(x^2+y^2+z^2\) (1)
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}\) = \(\dfrac{x+y+z}{1}\) = \(x+y+z\)
\(\dfrac{x}{a}\) = \(x+y+z\) ⇒ \(\dfrac{x^2}{a^2}\) = (\(x+y+z\))2 (2)
Từ (1) và (2) ta có :
\(\dfrac{x^2}{a^2}\) = \(x^2\) + y2 + z2 = ( \(x+y+z\))2 (đpcm)
⇒
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
= = = = = (1)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
= =
= ⇒ = ()2 (2)
Từ (1) và (2) ta có :
= + y2 + z2 = ( )2 (đpCm)

\(2,\\ a,=-3x^3y^3z^4\\ b,=\dfrac{1}{4}xy^2\cdot\dfrac{1}{4}x^4y^4\cdot\left(-\dfrac{4}{5}yz^2\right)=-\dfrac{1}{20}x^5y^7z^2\\ c,=-\dfrac{15}{14}x^6y^{11}z^{10}\\ 3,\\ a,=9\left(-1\right)\left(-\dfrac{1}{27}\right)=\dfrac{1}{3}\\ b,=-\dfrac{1}{5}\left(-8\right)=\dfrac{8}{5}\\ c,=\dfrac{4}{9}a\cdot36\left(-1\right)=-16a\)
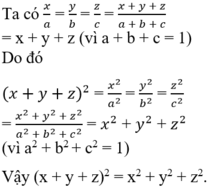
Thay x = 1; y = 1; z = 1 vào A
có: A = a.12.12.12 + b.12.1 + c.1.1.1
A = a + b + c = 2003
KL: A = 2003 tại x = 1;y = 1;z =1