DH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
6 tháng 4 2023
a)
`a<b`
`<=>3a<3b`
`<=>3a-5<3b-5`
b)
`a<b`
`<=>-8a> -8b`
`<=>-8a-3> -8b-3`
c)
`a<b`
`<=>4a<4b`
`<=>4a+9<4b+9`
mà `4a-7<4a+9`
`<=>4a-7<4b+9`
AH
Akai Haruma
Giáo viên
7 tháng 2 2022
Lời giải:
Gọi số hs lớp 8A là $a$ thì số hs lớp 8B là: $a-2-2=a-4$ (hs)
Theo bài ra ta có:
$a-4-5=(a+5)\frac{2}{3}$
$\Leftrightarrow a-9=\frac{2}{3}(a+5)$
$\Leftrightarrow 3(a-9)=2(a+5)$
$\Leftrightarrow a=37$ (hs)
Vậy số hs lớp 8A là $37$, số hs lớp 8B là $37-4=33$ (hs)
KB
26 tháng 2 2019
Đặt PT đã cho ở đề là A
Ta có : \(\sqrt{3a^2+8b^2+14ab}=\sqrt{3a\left(a+4b\right)+2b\left(a+4b\right)}=\sqrt{\left(3a+2b\right)\left(a+4b\right)}\)
\(\le\dfrac{3a+2b+a+4b}{2}=\dfrac{4a+6b}{2}=2a+3b\)
\(\Rightarrow\dfrac{a^2}{\sqrt{3a^2+8b^2+14ab}}\ge\dfrac{a^2}{2a+3b}\)
Làm tương tự như trên , ta có :
\(\dfrac{b^2}{\sqrt{3b^2+8c^2+14bc}}\ge\dfrac{b^2}{2b+3c};\dfrac{c^2}{\sqrt{3c^2+8a^2+14ac}}\ge\dfrac{c^2}{2c+3a}\)
Nên : \(A\ge\dfrac{a^2}{2a+3b}+\dfrac{b^2}{2b+3c}+\dfrac{c^2}{2c+3a}\ge\dfrac{\left(a+b+c\right)^2}{5\left(a+b+c\right)}=\dfrac{5}{a+b+c}\left(đpcm\right)\)
8 tháng 12 2017
Chứng minh BĐT phụ: \(\frac{m^2}{x}+\frac{n^2}{y}\ge\frac{\left(m+n\right)^2}{x+y}\) với \(x;y>0\) (*)
Ta có: \(3a^2+8b^2+14ab\)
\(=\left(3a^2+12ab\right)+\left(2ab+8b^2\right)\)
\(=3a\left(a+4b\right)+2b\left(a+4b\right)\)
\(=\left(3a+2b\right)\left(a+4b\right)\)
\(\Rightarrow\sqrt{3a^2+8b^2+14ab}=\sqrt{\left(3a+2b\right)\left(a+4b\right)}\le\frac{3a+2b+a+4b}{2}=2a+3b\)
\(\Rightarrow\frac{a^2}{\sqrt{3a^2+8b^2+14ab}}\ge\frac{a^2}{2a+3b}\)
Tương tự, ta có: \(\frac{b^2}{\sqrt{3b^2+8c^2+14bc}}\ge\frac{b^2}{2b+3c}\)
\(\frac{c^2}{\sqrt{3c^2+8a^2+14ca}}\ge\frac{c^2}{2c+3a}\)
Áp dụng (*), ta có:
\(VT\ge\frac{a^2}{2a+3b}+\frac{b^2}{2b+3c}+\frac{c^2}{2c+3a}\ge\frac{\left(a+b+c\right)^2}{2a+3b+2b+3c+2c+3a}=\frac{\left(a+b+c\right)^2}{5\left(a+b+c\right)}\)
\(=\frac{1}{5}\left(a+b+c\right)\)
Vậy \(\frac{a^2}{\sqrt{3a^2+8b^2+14ab}}+\frac{b^2}{\sqrt{3b^2+8c^2+14bc}}+\frac{c^2}{\sqrt{3c^2+8a^2+14ca}}\ge\frac{1}{5}\left(a+b+c\right)\)
16 tháng 12 2016
có thể là bé hơn hoặc bằng,các bạn thử cho mình với nhé
17 tháng 8 2020
áp dụng Bất Đẳng Thức CBS \(\sqrt{3a^2+8b^2+14ab}=\sqrt{\left(a+4b\right)\left(3a+2b\right)}\le\frac{1}{2}\left(4a+6b\right)\)
(BĐT CBS) do đó ta \(\Rightarrow\frac{a^2}{\sqrt{3a^2+8b^2+14ab}}\ge\frac{a^2}{2a+3b}\)
tương tư với mẫu còn lại
\(\Rightarrow\Sigma\frac{a^2}{\sqrt{3a^2+8b^2+14ab}}\ge\Sigma\frac{a^2}{2a+3b}\ge\frac{\left(a+b+c\right)^2}{5\left(a+b+c\right)}=\frac{a+b+c}{5}\left(Q.E.D\right)\)
đẳng thức xảy ra khi a=b=c
DT
Đỗ Thanh Hải
CTVVIP
18 tháng 3 2021
Gọi số học sinh lớp 8A là a
Số học sinh lớp 8B là b (đơn vị học sinh)(a,b \(\in N\)*)
Theo bài ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-2=b+2\\b-5=\dfrac{2}{3}\left(a+5\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a-b=4\\\dfrac{2}{3}a-b=-\dfrac{25}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=37\\b=33\end{matrix}\right.\left(tmđk\right)\)
Vậy số học sinh lớp 8A là 37 học sinh
số học sinh lớp 8B là 33 học sinh
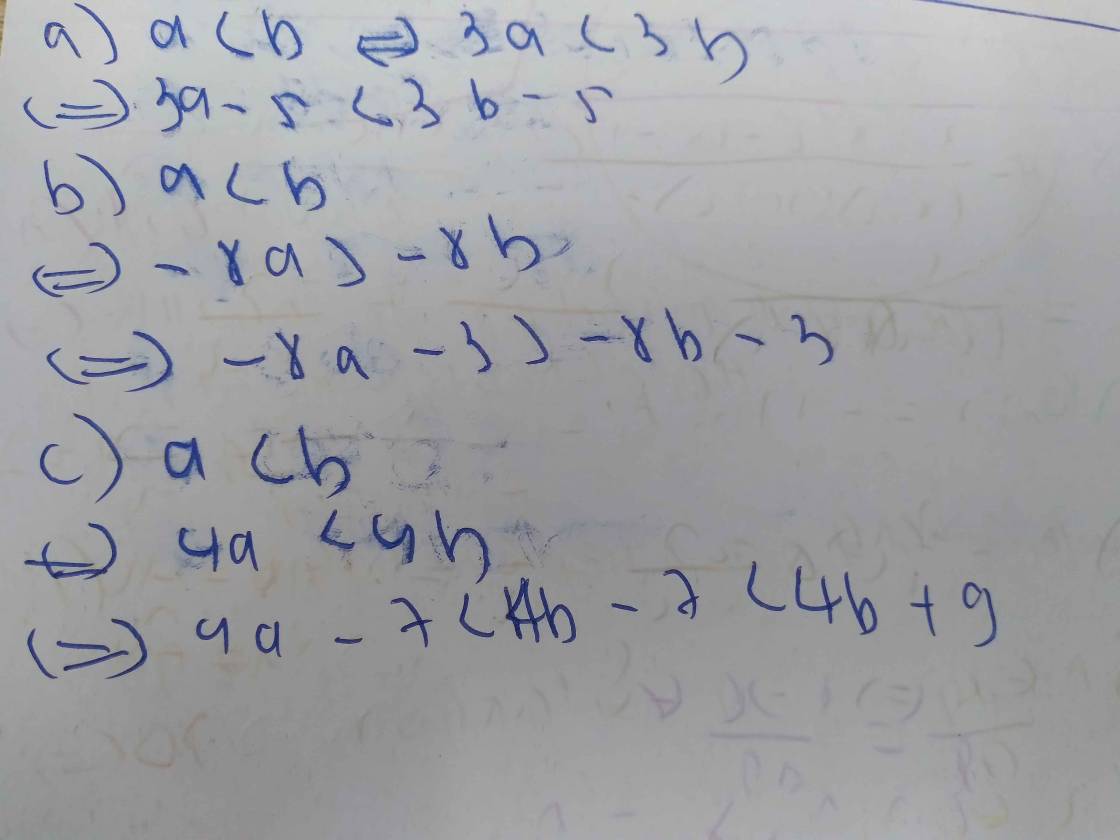
a) Vì a>b
=>3a>3b
=>5-3a<5-3b
c) vì a>b
=>8a>8b
=>8a-3>8b-3
c) vì a>b
=>8a>8b
Vì 3<5
=>8a-3<8b-5