Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

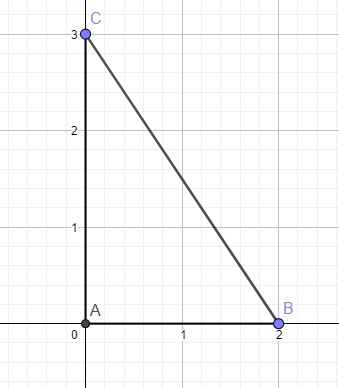
Dựng tam giác ABC vuông tại A, trong đó \(AB=2\left(cm\right)\) và \(AC=3\left(cm\right)\)
Khi đó \(tan\widehat{ABC}=\dfrac{AC}{AB}=\dfrac{3}{2}\)
Vậy \(\widehat{ABC}\) chính là góc nhọn \(\alpha\) cần dựng

\(\text{Ta có: }x=\sqrt{\frac{3-\sqrt{5}}{3+\sqrt{5}}}=\sqrt{\frac{\left(3-\sqrt{5}\right)^2}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}}=\frac{3-\sqrt{5}}{\sqrt{9-5}}=\frac{3-\sqrt{5}}{2}.\)
\(A=x^5-6x^4+12x^3-4x^2-13x+2020\)
\(=\left(x^5-3x^4+x^3\right)-\left(3x^4-9x^3+3x^2\right)+\left(2x^3-6x^2+2x\right)+\left(5x^2-15x+5\right)+2015\)
\(=x^3\left(x^2-3x+1\right)-3x^2\left(x^2-3x+1\right)+2x\left(x^2-3x+1\right)+5\left(x^2-3x+1\right)+2015\)
\(=\left(x^2-3x+1\right)\left(x^3-3x^2+2x+5\right)+2015\)
Thay x vào A ta có:
\(A=\left[\left(\frac{3-\sqrt{5}}{2}\right)^2-3.\frac{3-\sqrt{5}}{2}+1\right]\left(.....\right)+2015\)
\(=\left(\frac{14-6\sqrt{5}}{4}-\frac{9-3\sqrt{5}}{2}+1\right)\left(....\right)+2015\)
\(=0\cdot\left(......\right)+2015=2015\)
Vậy.....

\(3x^3-7x^2+17x-5=3x^3-x^2-6x^2+2x+15x-5\)
\(=x^2\left(3x-1\right)-2x\left(3x-1\right)+5\left(3x-1\right)\)
\(=\left(3x-1\right)\left(x^2-2x+5\right)\)
\(x^3-x^2-4=x^3+x^2+2x-2x^2-2x-4\)
\(=x\left(x^2+x+2\right)=2\left(x^2+x+2\right)=\left(x-2\right)\left(x^2+x+2\right)\)
Lời giải:
$a=2+\sqrt{5}$
$a-2=\sqrt{5}$
$a^2-4a+4=5\Leftrightarrow a^2-4a-1=0$
$p(a)=a^5-13a^4+7a^3-4a^2-6a$
$=a^3(a^2-4a-1)-9a^2(a^2-4a-1)-28a(a^2-4a-1)-125a^2-34a$
$=-125a^2-34a=-125(a^2-4a-1)-534a-125$
$=-534a-125=-534(2+\sqrt{5})-125=-1193-534\sqrt{5}$