HA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 7 2017
ta co \(sin^2a+cos^2a=1\Rightarrow cosa=0.36\)
\(\frac{sina}{cosa}=tana\Rightarrow tana=\frac{20}{9}\)
\(tana\cdot cotga=1\Rightarrow cotga=\frac{9}{20}\)
câu b tương tự nha cau c \(\frac{sina+cosa}{sina-cosa}=\) bn
TA
21 tháng 7 2021
`sin^2 α+cos^2α=1`
`<=> (2/3)^2+cos^2α=1`
`=> cosα= \sqrt5/3`
`=> tan α=(sinα)/(cosα) = (2\sqrt5)/5`
`=> cota = 1/(tanα)=sqrt5/2`
CM
13 tháng 8 2017
*Cách dựng: hình d
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 2 đơn vị dài
- Trên tia Oy dựng đoạn OB bằng 1 đơn vị dài
LH
2
TA
4 tháng 8 2021
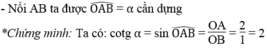
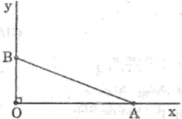
`sin^2 α+cos^2 α =1`
`=> sinα =\sqrt(1-cos^2α)=\sqrt(1-(3/4)^2) = \sqrt7/4`
`=> tanα=(sinα)/(cosα)=(3\sqrt7)/7`
`=> cotα=1/(tanα)=\sqrt7/3`
4 tháng 8 2021
Đề bài cho cos rồi tính cos làm gì nhỉ =))) Mình tính sin thay vào chỗ đấy nhé.
-------------------------------------------------------------------------------------------------------
\(cos\alpha=\dfrac{3}{4}\Rightarrow cos^2\alpha=\dfrac{9}{16}\)
Mà \(sin^2\alpha+cos^2\alpha=1\)
\(\Rightarrow sin^2\alpha=1-cos^2\alpha=1-\dfrac{9}{16}=\dfrac{7}{16}\)
\(\Rightarrow cos\alpha=\dfrac{\sqrt{7}}{4}\\ \Rightarrow tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{\dfrac{3}{4}}{\dfrac{\sqrt{7}}{4}}=\dfrac{3\sqrt{7}}{7}\\ \Rightarrow cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{\sqrt{7}}{3}\)
CM
21 tháng 6 2017
*Cách dựng:
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 3 đơn vị dài
- Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B
TN
2
CM
21 tháng 1 2019
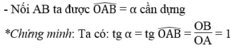
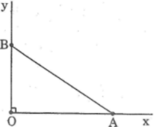
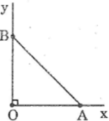
sin α = 0,25 = 14
*Cách dựng: hình a
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 1 đơn vị dài
- Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B
PT
1
CM
4 tháng 1 2017
Dựng tam giác vuông có cạnh huyền bằng 3, một cạnh góc vuông có độ dài bằng 2, khi đó góc kề cạnh góc vuông có độ dài bằng 2 là góc α cần dựng
Ta có: cosα = 2 3 => α ≈ 48 0 11 '
Dựng tam giác ABC vuông tại A, trong đó \(AB=2\left(cm\right)\) và \(AC=3\left(cm\right)\)
Khi đó \(tan\widehat{ABC}=\dfrac{AC}{AB}=\dfrac{3}{2}\)
Vậy \(\widehat{ABC}\) chính là góc nhọn \(\alpha\) cần dựng