
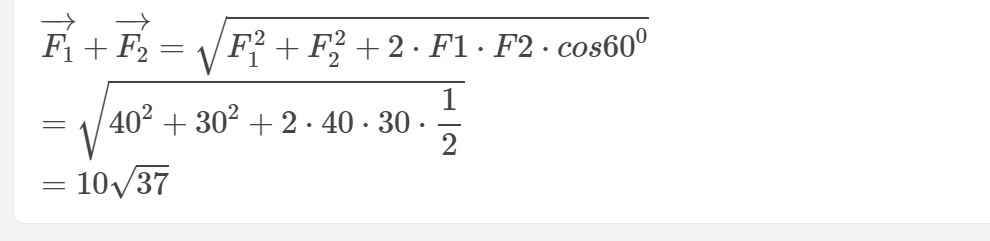
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

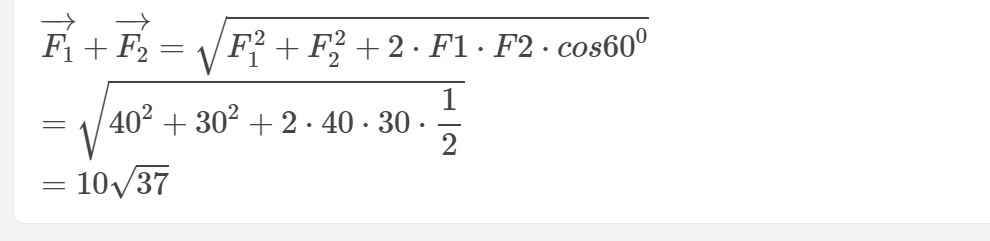

Sửa đề: F1=40N
\(\overrightarrow{F_1}+\overrightarrow{F_2}=\sqrt{F_1^2+F_2^2+2\cdot F1\cdot F2\cdot cos60^0}\)
\(=\sqrt{40^2+30^2+2\cdot40\cdot30\cdot\dfrac{1}{2}}\)
\(=10\sqrt{37}\)


Ta có: \(\overrightarrow{F}=\overrightarrow{F1}+\overrightarrow{F2}\) (1)
\(\Rightarrow\) \(F=\sqrt{F1^2+F2^2+2F1\cdot F2\cdot cos60^o}\) (Bình phương 2 vế của (1) r biến đổi vectơ F1, F2)
Chúc bn học tốt!

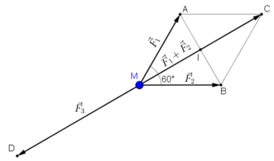
Ta biểu diễn 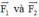 bằng hai vec tơ
bằng hai vec tơ 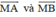 như hình vẽ.
như hình vẽ.
Khi đó 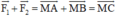 (C là đỉnh còn lại của hình bình hành MACB).
(C là đỉnh còn lại của hình bình hành MACB).
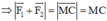
+ Tính MC : Gọi I là trung điểm của AB ⇒ I là trung điểm của MC.
Δ MAB có MA = MB = 100 và góc AMB = 60º nên là tam giác đều
⇒ đường cao 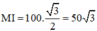
⇒ MC = 2.MI = 100√3.
Vec tơ 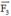 là vec tơ đối của
là vec tơ đối của 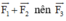 có hướng ngược với
có hướng ngược với 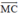 và có cường độ bằng 100√3N.
và có cường độ bằng 100√3N.

Gọi O là giao điểm của giá hợp lực
F và AB
Hai lực \(F_1;F_2\)cùng chiều
Điểm đặt O trong khoảng AB :
+ Ta có :
\(\hept{\begin{cases}\frac{OA}{AB}\\OA+OB=AB=4cm\end{cases}}=\frac{F_2}{F_1}\)\(=3\)
\(\hept{\begin{cases}OA=3cm\\OB=1cm\end{cases}}\)
Vậy F có giá qua O cách A 3 cm , cachs B 1 cm , cùng chiều với \(F_1;F_2\)và có độ lớn \(F=8N\)