
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 4:
D và F cùng nhìn AC dưới 1 góc vuông nên tứ giác ACDF nội tiếp
\(\Rightarrow\widehat{ADF}=\widehat{ACF}\) (cùng chắn AF)
Tương tự, ABDE nội tiếp \(\Rightarrow\widehat{ABE}=\widehat{ADE}\) (cùng chắn AE)
Lại có \(\widehat{ABE}=\widehat{ACF}\) (cùng phụ góc \(\widehat{A}\))
\(\Rightarrow\widehat{ADE}=\widehat{ADF}\) hay AD là phân giác góc \(\widehat{FDE}\)
./
Hoàn toàn tương tự, ta cũng có CF là phân giác \(\widehat{DFE}\Rightarrow\widehat{BFD}=\widehat{AFE}\)
Mà \(\widehat{AFE}=\widehat{BFK}\Rightarrow\widehat{BFK}=\widehat{BFD}\)
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{FK}{FD}\) theo định lý phân giác
Đồng thời \(\dfrac{CK}{CD}=\dfrac{FK}{FD}\) (CF là phân giác ngoài góc \(\widehat{DFK}\))
\(\Rightarrow\dfrac{BK}{BD}=\dfrac{CK}{CD}\Rightarrow\dfrac{BK}{CK}=\dfrac{BD}{CD}\)
Qua B kẻ đường thẳng song song AC cắt AK và AD tại P và Q
Theo Talet: \(\dfrac{BK}{CK}=\dfrac{BP}{AC}\) đồng thời \(\dfrac{BD}{DC}=\dfrac{BQ}{AC}\)
\(\Rightarrow\dfrac{BP}{AC}=\dfrac{BQ}{AC}\Rightarrow BP=BQ\)
Mặt khác BP song song MF (cùng song song AC)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{AF}{AB}\) ; \(\dfrac{NF}{BQ}=\dfrac{AF}{AB}\) (Talet)
\(\Rightarrow\dfrac{MF}{BP}=\dfrac{NF}{BQ}\Rightarrow MF=NF\)

\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-1\end{matrix}\right.\)
8: \(=\dfrac{x_1^2+x_2^2}{\left(x_1\cdot x_2\right)^2}=\dfrac{2}{1}=2\)
9: \(=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=2^3-3\cdot\left(-1\right)\cdot2=8+6=14\)
16: \(=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{2^2-4\cdot\left(-1\right)}=\sqrt{4+4}=2\sqrt{2}\)

1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)

III:
1) \(x-y=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\)
2) \(x-1=\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)
4) \(a-2\sqrt{a}+1=\left(\sqrt{a}-1\right)^2\)
5) \(2x-\sqrt{x}-3=\left(\sqrt{x}+1\right)\left(2\sqrt{x}-3\right)\)
6) \(6a^2-5a\sqrt{b}-b=\left(a-\sqrt{b}\right)\left(6a+\sqrt{b}\right)\)
7) \(x-2\sqrt{x-1}-y^2=\left(\sqrt{x-1}-1\right)^2-y^2=\left(\sqrt{x-1}-1-y\right)\left(\sqrt{x-1}-1+y\right)\)
II:
2.8) ĐKXĐ: \(x\ge2\)
2.9: ĐKXĐ: \(\left[{}\begin{matrix}x< \dfrac{1}{2}\\\dfrac{1}{2}< x\le1\end{matrix}\right.\)
2.10: ĐKXĐ: \(x\ne0\)
2.11: ĐKXĐ: \(\left[{}\begin{matrix}x\le-5\\x\ge3\end{matrix}\right.\)

\(7,\\ a,ĐK:a>0;a\ne1\\ b,K=\dfrac{a-1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{\sqrt{a}-1+2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\\ K=\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}=\dfrac{a-1}{\sqrt{a}}\\ c,a=3+2\sqrt{2}=\left(\sqrt{2}+1\right)^2\\ \Leftrightarrow K=\dfrac{3+2\sqrt{2}-1}{\sqrt{2}+1}=\dfrac{2+2\sqrt{2}}{\sqrt{2}+1}=\dfrac{2\left(\sqrt{2}+1\right)}{\sqrt{2}+1}=2\\ d,K< 0\Leftrightarrow a-1< 0\left(\sqrt{a}>0\right)\Leftrightarrow0< a< 1\)



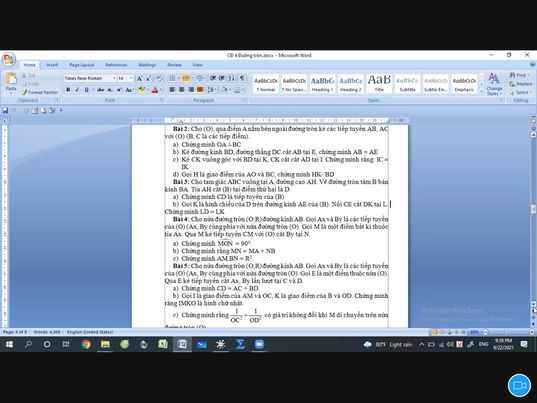

 Mình đang cần rất gấp từ câu 7 đến câu 21. Mọi người giải giúp mình. Mình cảm ơn !
Mình đang cần rất gấp từ câu 7 đến câu 21. Mọi người giải giúp mình. Mình cảm ơn !


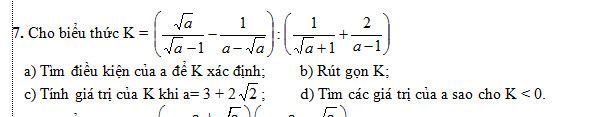
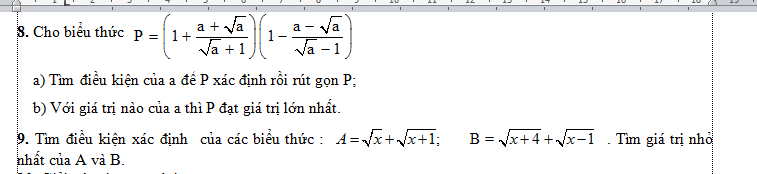
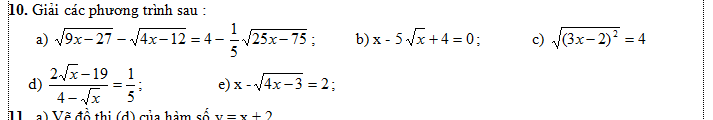
bài 7
A=\(\dfrac{x+2}{\sqrt{x^3}-1}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(x+\sqrt{x}+1\right)}+\dfrac{-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
A=\(\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
A=\(\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)=\(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+x+1\right)}\)
A=\(\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
bài 8
P=\(\left[\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)^2}\right].\dfrac{\left(x-1\right)^2}{4x}\)
P=\(\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)}.\dfrac{\left(x-1\right)^2}{4x}\)
P=\(\dfrac{2\sqrt{x}}{\left(x-1\right)\left(\sqrt{x}-1\right)}.\dfrac{\left(x-1\right)^2}{4x}\)=\(\dfrac{x-1}{2\sqrt{x}\left(\sqrt{x}-1\right)}\)
P=\(\dfrac{\sqrt{x}+1}{2\sqrt{x}}\)
bài 9
P=\(\left[\dfrac{2\sqrt{xy}}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}-\dfrac{\sqrt{x}+\sqrt{y}}{2\left(\sqrt{x}-\sqrt{y}\right)}\right].\dfrac{2\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{4\sqrt{xy}-\left(\sqrt{x}+\sqrt{y}\right)^2}{2\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}.\dfrac{2\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{2\sqrt{xy}-x-y}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}.\dfrac{\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{-\left(\sqrt{x}-\sqrt{y}\right)^2}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}.\dfrac{\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{-\sqrt{x}}{\sqrt{x}+\sqrt{y}}\)
bài 10
P=\(\left[\dfrac{1}{\sqrt{x}+2}-\dfrac{2}{\left(\sqrt{x}+2\right)^2}\right]:\left[\dfrac{2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{1}{\sqrt{x}-2}\right]\)
P=\(\dfrac{\sqrt{x}+2-2}{\left(\sqrt{x}+2\right)^2}:\dfrac{2-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
P=\(\dfrac{\sqrt{x}}{\left(\sqrt{x}+2\right)^2}.\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{-\sqrt{x}}\)=\(\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+2}\)
cảm ơn bạn nha