Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
D = ST = 2m;
a) tìm dtối biết d = 20 cm và SM = 50 cm.
b) MM1 =? Để d’tối = ½ dtối.
c) v = 2m/s tìm Vtối =?
d) vật sáng d1 =8cm. Tìm SM để dtối . Tìm Stối và Snửa tối.
Bài giải:
a) Ta có hình vẽ:
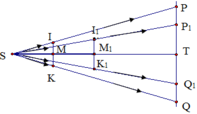
a) Bán kính vùng tối trên tường là PT. ST = 2m = 200 cm.
∆SIM và ∆SPT là 2 tam giác vuông đồng dạng nên bán kính vùng tối là
⇒ I M P T = S M S T ⇔ P T = S T S M . I M = 200 50 . d 2 = 40 c m
Vậy đường kính vùng tối là dtối = 2.PT = 80 cm
b) Từ hình vẽ ta thấy để bán kính vùng tối giảm xuống ta phải di chuyển tấm bìa về phía tường đến vị trí M1
Gọi P1T là bán kính bóng đen lúc này P1T = 1/2PT = 20 cm
∆SIM và ∆SPT là 2 tam giác vuông đồng dạng nên
⇒ I 1 M 1 P 1 T = S M 1 S T ⇔ S M 1 = I 1 M 1 P 1 T . S T = 20 40 .200 = 100
Vậy cần di chuyển tấm bìa về phía tường một đoạn
M1M = SM1 - SM = 100-50=50 cm.
c) Khi tấm bìa di chuyển đều với vận tốc v = 2m/s = 200 cm/s
và đi được quãng đường M1M = 50cm
thì mất thời gian t = M 1 M v = 50 200 = 0 , 25 ( s ) .
Cũng trong khoảng thời gian đó đường kính của vùng tối thay đổi một đoạn là
PP1 = PT – P1T = 80– 40 = 40 cm
Vậy tốc độ thay đổi của bán kính vùng tối là
V’ = P 1 P t = 40 0 , 25 = 160 c m / s = 1 , 6 m / s
d)
|
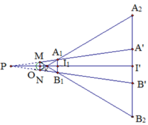
Gọi O là tâm, MN là đường kính vật sáng hình cầu, P là giao của MA’ và NB’ Ta có Δ P A 1 B 1 ~ Δ P A ' B ' ⇒ P I 1 P I ' = A 1 B 1 A ' B ' = 20 80 = 1 4 ⇒ 4 P I 1 = P I ' = P I 1 + I I ' ⇒ 3 P I 1 = I 1 I ' ⇒ P I 1 = I 1 I ' 3 = 100 3 c m
|
Ta lại có:
Δ P M N ~ Δ P A 1 B 1 ⇒ P O P I 1 = M N A 1 B 1 = 8 20 = 2 5 ⇒ P O = 2 5 P I ⇒ P O = 2 5 . 100 3 = 40 3 c m
mà OI1 = PI1 – PO = 100 3 − 40 3 = 60 3 = 20 c m .
Vậy cần đặt đĩa chắn sáng cách tâm vật sáng hình cầu là 20 cm
*) Gọi K là giao điểm của NA2 và MB2
Ta có
Δ K M N ~ Δ K A 1 B 1 ⇒ KO KI 1 = MN A 1 B 1 = 8 20 = 2 5 ⇒ KO = 2 5 KI 1 = 2 5 (OI 1 - OK) = 2 5 OI 1 - 2 5 OK ⇒ 2 5 O I 1 = 7 5 O K ⇒ O K = 2 7 O I 1 = 40 7 c m ⇒ K I 1 = 5 2 O K = 100 7 c m
Mặt khác ta có:
Δ K A 1 B 1 ~ Δ K A 2 B 2 ⇒ K I 1 K I ' = A 1 B 1 A 2 B 2 ⇒ A 2 B 2 = K I ' K I 1 A 1 B 1 = K I 1 + I 1 I ' K I 1 A 1 B 1 = 100 7 + 100 100 7 20 = 160 c m
Vậy diện tích vùng nửa tối là:
S = π . A 2 B 2 2 4 − π . A ' B ' 2 4 = π 4 ( A 2 B 2 2 − A ' B ' 2 ) = 3.14 4 ( 160 2 − 80 2 ) = 15.72 c m 2

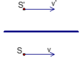
a) Trường hợp S chuyển động song song với gương.
Vì S’ đối xứng với S qua gương nên vận tốc của S’ đối với gương cócùng độ lớn, song song và cùng chiều với v đối với gương. Còn vận tốc của S’ đối với S bằng 0.
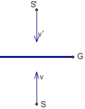
b) Trường hợp S chuyển động vuông góc với gương.
Vận tốc của S’ đối với gương có cùng độ lớn, cùng phương và ngược chiều với v. Vận tốc của S’ đối với S cùng phương và ngược chiều và có độ lớn bằng 2v.
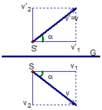
c) S chuyển động theo phương hợp với mặt phẳng gương một góc α
Lúc này có thể coi S vừa chuyển động song song với gương (với vận tốc v1), vừa chuyển động vuông góc với gương (với vận tốc v2)
Ta có v1 = v.cosα và v2 = v.sinα
Vậy vận tốc của S’ đối với gương là v1 = v.cosα còn vận tốc của S’ đối với S là 2.v2 = 2v.sinα theo phương vuông góc với gương

Vẽ hình:
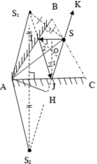
a) S1 là ảnh của S qua gương AB => S1 đối xứng với S qua AB
S2 là ảnh của S1 qua gương AC => S2 đối xứng với S 1 qua AC
Ta nối S2 với S cắt AC tại J, nối J với S1 cắt AB tại I
=> SI, IJ, JS là ba đoạn của tia sáng cần dựng.
b) Dựng hai phỏp tuyến tại I và J cắt nhau tai O
Góc tạo bởi tia phản xạ JK và tia tới SI là ∠ ISK
Theo tính chất góc ngoài tam giác ta có
I S K ^ = I ^ + J ^ = 2 I ^ 2 + 2 J ^ 2 = 2 ( 180 0 − I O ^ J ) = 2. B A ^ C = 120 0
c) Tổng độ dài ba đoạn:
SI + IJ + JS = S1I + IJ + JS = S1J + JS = S2J + JS = S2S
(Đối xứng trục)
Vậy SI + IJ + JS = S2S
Ta có:
∠ S1AS = 2 ∠ S1AB (1)
∠ S1AS2 = 2 ∠ S1AC (2)
Lấy (2) – (1):
∠ S1AS2 - ∠ S1AS = 2( ∠ S1AC - ∠ S1AB)
ð ∠ SAS2 = 2 ∠ BAC
ð ∠ SAS2 = 1200
Xét tam giác cân SAS2 tại A, có ∠ A = 1200
ð ∠ ASH = ∠ AS2H = 300 với đường cao AH, ta có: SS2 = 2SH
Xét tam giác vuông SAH taị H có ∠ ASH = 300 ta có: AH = AS/2
Trong tam giác vuông SAH tại H.
Theo định lí pitago ta tính được SH= S A . 3 2
nên SS2 = 2SH = 2. S A . 3 2 = SA 3
=> SS2 nhỏ nhất ó SA nhỏ nhất ó AS là đường cao của tam giác đều ABC
ó S là trung điểm của BC.
mấy dòng cúi đọc chả hiểu j nhưng mình vẫn chép
thank you so much
I LOVE YOU chụt chụt...

TRẢ LỜI:
a) Trường hợp S chuyển động song song với gương.
Vì S’ đối xứng với S qua gương nên vận tốc của S’ đối với gương cócùng độ lớn, song song và cùng chiều với v đối với gương. Còn vận tốc của S’ đối với S bằng 0.
b) Trường hợp S chuyển động vuông góc với gương.
Vận tốc của S’ đối với gương có cùng độ lớn, cùng phương và ngược chiều với v. Vận tốc của S’ đối với S cùng phương và ngược chiều và có độ lớn bằng 2v.
c) S chuyển động theo phương hợp với mặt phẳng gương một góc α
Lúc này có thể coi S vừa chuyển động song song với gương (với vận tốc v1), vừa chuyển động vuông góc với gương (với vận tốc v2)
Ta có v1 = v.cosα và v2 = v.sinα
Vậy vận tốc của S’ đối với gương là v1 = v.cosα còn vận tốc của S’ đối với S là 2.v2 = 2v.sinα theo phương vuông góc với gương
Bạn nhớ cho mình 1 like nhé !

a) Hiệu điện thế:
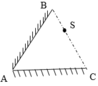
- Vì điểm A và B nằm trên cùng một mặt phẳng thế nên điện thế giữa hai điểm đó là như nhau, do đó: UAB = 0.
- Ta có UAC = E.AC = 1000.0,08 = 80 V.
- Tương tự:UBC=E.AC=1000.0,08=80V.UBC=E.AC=1000.0,08=80V.b) Lực điện trường là loại lực thế nên công của chúng không phụ thuộc vào đường đi, do đó:
A=|e|UBC=|e|UACA=|e|UBC=|e|UAC=1,6.10−19.80=12,8.10−18J.=1,6.10−19.80=12,8.10−18J.c) Công của lực điện trường bằng độ biến thiên động năng của êlectron:
AAC=mv2C//2−mv20/2
⇒vC=√2AACm=√2.128.10−199,1.10−31⇒vC=2AACm=2.128.10−199,1.10−31≈5,3.106m/s.