Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

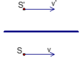
a) Trường hợp S chuyển động song song với gương.
Vì S’ đối xứng với S qua gương nên vận tốc của S’ đối với gương cócùng độ lớn, song song và cùng chiều với v đối với gương. Còn vận tốc của S’ đối với S bằng 0.
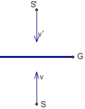
b) Trường hợp S chuyển động vuông góc với gương.
Vận tốc của S’ đối với gương có cùng độ lớn, cùng phương và ngược chiều với v. Vận tốc của S’ đối với S cùng phương và ngược chiều và có độ lớn bằng 2v.
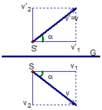
c) S chuyển động theo phương hợp với mặt phẳng gương một góc α
Lúc này có thể coi S vừa chuyển động song song với gương (với vận tốc v1), vừa chuyển động vuông góc với gương (với vận tốc v2)
Ta có v1 = v.cosα và v2 = v.sinα
Vậy vận tốc của S’ đối với gương là v1 = v.cosα còn vận tốc của S’ đối với S là 2.v2 = 2v.sinα theo phương vuông góc với gương

a, 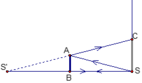
Xét sự phản xạ ánh sáng nằm trong mặt phẳng thẳng đứng
Ta có S’ là ảnh của Svà đối xứng với S qua gương, ∆ S’SC có AB là đường trung bình nên SC = 2Ab = 2a.
Tương tự với các cạnh còn lại vậy vệt sáng trên tường là hình vuông có cạnh =2a
b, 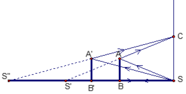
Khi nguồn sáng S ở sát chân tườngvà di chuyển gương theo phương vuông góc với tường(đến gần hoặc ra xa tường)thì kích thước của vệt sáng không thay đổi. Luôn là hinhg vuông cạnh là 2a. Vì SC luôn bằng 2AB = 2a
Trong khoảng thời gian t gương di chuyển với vận tốc v và đi được quãng đường BB’ = vt.
Cũng trong thời gian đó ảnh S’ của S dịch chuyển với vận tốc v’ và đi được quãng đường S’S” = v’t
Theo tính chất ảnh và vật đối xứng nhau qua gương ta có:
SB’ = B’S” <=>SB + BB’ = B’S’+S’S” (1)
SB = BS’ <=> SB = BB’ + B’S’ (2)
Thay (2) và (1) ta có: BB’ + B’S’+ BB’ = B’S’+S’S” <=> 2BB’ = S’S”
Hay v’t = 2vt <=> v’ =2v

Tóm tắt:
D = ST = 2m;
a) tìm dtối biết d = 20 cm và SM = 50 cm.
b) MM1 =? Để d’tối = ½ dtối.
c) v = 2m/s tìm Vtối =?
d) vật sáng d1 =8cm. Tìm SM để dtối . Tìm Stối và Snửa tối.
Bài giải:
a) Ta có hình vẽ:
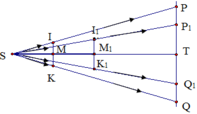
a) Bán kính vùng tối trên tường là PT. ST = 2m = 200 cm.
∆SIM và ∆SPT là 2 tam giác vuông đồng dạng nên bán kính vùng tối là
⇒ I M P T = S M S T ⇔ P T = S T S M . I M = 200 50 . d 2 = 40 c m
Vậy đường kính vùng tối là dtối = 2.PT = 80 cm
b) Từ hình vẽ ta thấy để bán kính vùng tối giảm xuống ta phải di chuyển tấm bìa về phía tường đến vị trí M1
Gọi P1T là bán kính bóng đen lúc này P1T = 1/2PT = 20 cm
∆SIM và ∆SPT là 2 tam giác vuông đồng dạng nên
⇒ I 1 M 1 P 1 T = S M 1 S T ⇔ S M 1 = I 1 M 1 P 1 T . S T = 20 40 .200 = 100
Vậy cần di chuyển tấm bìa về phía tường một đoạn
M1M = SM1 - SM = 100-50=50 cm.
c) Khi tấm bìa di chuyển đều với vận tốc v = 2m/s = 200 cm/s
và đi được quãng đường M1M = 50cm
thì mất thời gian t = M 1 M v = 50 200 = 0 , 25 ( s ) .
Cũng trong khoảng thời gian đó đường kính của vùng tối thay đổi một đoạn là
PP1 = PT – P1T = 80– 40 = 40 cm
Vậy tốc độ thay đổi của bán kính vùng tối là
V’ = P 1 P t = 40 0 , 25 = 160 c m / s = 1 , 6 m / s
d)
|
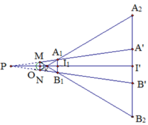
Gọi O là tâm, MN là đường kính vật sáng hình cầu, P là giao của MA’ và NB’ Ta có Δ P A 1 B 1 ~ Δ P A ' B ' ⇒ P I 1 P I ' = A 1 B 1 A ' B ' = 20 80 = 1 4 ⇒ 4 P I 1 = P I ' = P I 1 + I I ' ⇒ 3 P I 1 = I 1 I ' ⇒ P I 1 = I 1 I ' 3 = 100 3 c m
|
Ta lại có:
Δ P M N ~ Δ P A 1 B 1 ⇒ P O P I 1 = M N A 1 B 1 = 8 20 = 2 5 ⇒ P O = 2 5 P I ⇒ P O = 2 5 . 100 3 = 40 3 c m
mà OI1 = PI1 – PO = 100 3 − 40 3 = 60 3 = 20 c m .
Vậy cần đặt đĩa chắn sáng cách tâm vật sáng hình cầu là 20 cm
*) Gọi K là giao điểm của NA2 và MB2
Ta có
Δ K M N ~ Δ K A 1 B 1 ⇒ KO KI 1 = MN A 1 B 1 = 8 20 = 2 5 ⇒ KO = 2 5 KI 1 = 2 5 (OI 1 - OK) = 2 5 OI 1 - 2 5 OK ⇒ 2 5 O I 1 = 7 5 O K ⇒ O K = 2 7 O I 1 = 40 7 c m ⇒ K I 1 = 5 2 O K = 100 7 c m
Mặt khác ta có:
Δ K A 1 B 1 ~ Δ K A 2 B 2 ⇒ K I 1 K I ' = A 1 B 1 A 2 B 2 ⇒ A 2 B 2 = K I ' K I 1 A 1 B 1 = K I 1 + I 1 I ' K I 1 A 1 B 1 = 100 7 + 100 100 7 20 = 160 c m
Vậy diện tích vùng nửa tối là:
S = π . A 2 B 2 2 4 − π . A ' B ' 2 4 = π 4 ( A 2 B 2 2 − A ' B ' 2 ) = 3.14 4 ( 160 2 − 80 2 ) = 15.72 c m 2
TRẢ LỜI:
a) Trường hợp S chuyển động song song với gương.
Vì S’ đối xứng với S qua gương nên vận tốc của S’ đối với gương cócùng độ lớn, song song và cùng chiều với v đối với gương. Còn vận tốc của S’ đối với S bằng 0.
b) Trường hợp S chuyển động vuông góc với gương.
Vận tốc của S’ đối với gương có cùng độ lớn, cùng phương và ngược chiều với v. Vận tốc của S’ đối với S cùng phương và ngược chiều và có độ lớn bằng 2v.
c) S chuyển động theo phương hợp với mặt phẳng gương một góc α
Lúc này có thể coi S vừa chuyển động song song với gương (với vận tốc v1), vừa chuyển động vuông góc với gương (với vận tốc v2)
Ta có v1 = v.cosα và v2 = v.sinα
Vậy vận tốc của S’ đối với gương là v1 = v.cosα còn vận tốc của S’ đối với S là 2.v2 = 2v.sinα theo phương vuông góc với gương
Bạn nhớ cho mình 1 like nhé !