Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Do A',B',C' là trung điểm BC,CA,AB=> A'B' song song với AB,B'C'song song với BC,C'A' song song với CA
\(\overrightarrow{A'B'}=\left(6;3\right)\) => VTPT của đường thẳng AB là: \(\overrightarrow{n}=\left(1;-2\right)\)
và C' thuộc (AB)=>Phương trình đường thẳng AB là:
(AB): x-2y-6=0
Tương tự ta có phương trình đường thẳng BC là:
(BC): x+4=0
Tọa độ điểm B là nghiệm hệ
\(\left\{{}\begin{matrix}\text{x-2y-6=0}\\x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=-5\end{matrix}\right.\)
=>B(-4;-5)
A'(-4;1) là TĐ của BC => tọa độ C(-4;7)
C'(2;-2) là TĐ của AB =>tọa độ A(8;1)
b) Gọi tọa độ trọng tâm G của tam giác A'B'C' là G(x;y)
=>\(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=0\)
=>\(\left\{{}\begin{matrix}\left(-4-x\right)+\left(2-x\right)+\left(2-x\right)=0\\\left(1-y\right)+\left(4-y\right)+\left(-2-y\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
=>G(0;1)
Thay vào tính
Ta có:\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\) =(8-4-4;1-1+7-1-5-1)=(0;0)
=>G là trọng tâm tam giác ABC=>ĐPCM

A’ là trung điểm của cạnh BC nên -4 = (xB+ xC)
=> xB+ xC = -8 (1)
Tương tự ta có xA+ xC = 4 (2)
xB+ xC = 4 (3)
=> xA+ xB+ xC =0 (4)
Kết hợp (4) và (1) ta có: xA= 8
(4) và (2) ta có: xB= -4
(4) và (3) ta có: xC = -4
Tương tự ta tính được: yA = 1; yB = -5; yC = 7.
Vậy A(8;1), B(-4;-5), C(-4; 7).
Gọi G la trọng tâm tam giác ABC thì
xG= = 0; yG =
= 1 => G(0,1).
xG’= ; yG’ =
= 1 => G'(0;1)
Rõ ràng G và G’ trùng nhau.

a: vecto AB=(1;1)
vecto AC=(2;6)
vecto BC=(1;5)
b: \(AB=\sqrt{1^2+1^2}=\sqrt{2}\)
\(AC=\sqrt{2^2+6^2}=2\sqrt{10}\)
\(BC=\sqrt{1^2+5^2}=\sqrt{26}\)
=>\(C=\sqrt{2}+2\sqrt{10}+\sqrt{26}\)
c: Tọa độ trung điểm của AB là:
x=(1+2)/2=1,5 và y=(-1+0)/2=-0,5
Tọa độ trung điểm của AC là;
x=(1+3)/2=2 và y=(-1+5)/2=4/2=2
Tọa độ trung điểm của BC là:
x=(2+3)/2=2,5 và y=(0+5)/2=2,5
d: ABCD là hình bình hành
=>vecto AB=vecto DC
=>3-x=1 và 5-y=1
=>x=2 và y=4
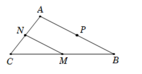
A’ là trung điểm của BC
B’ là trung điểm của AC
C’ là trung điểm của BA
Gọi G là trọng tâm ΔABC và G’ là trọng tâm ΔA’B’C’
Ta có :
Vậy G ≡ G’ (đpcm)