Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình a)
Ta có = 900,
+
= 900
mà =
( đối đỉnh)
Suy ra =
Vậy = 400
Hình b) Ta có +
= 900,
+
=900,
Suy ra =
Vậy = 250,
Hình c) Ta có: +
= 900,
+
= 900,
Suy ra =
Vậy = 600
Hình d) ta có
= 900 -
= 900 - 550 = 350
= 900 +
(Góc ngoài tam giác BKE)
= 900 + 350 = 1250

bài 96 :
a) = \(\left(1\frac{4}{23}-\frac{4}{23}\right)\) + \(\left(\frac{5}{21}+\frac{16}{21}\right)\) + 0,5 = 1+1+0,5 = 2,5
b) = \(\frac{3}{7}\) \(\left(19\frac{1}{3}-33\frac{1}{3}\right)\)= \(\frac{3}{7}\) . (-14) = -6
c)= \(\frac{1}{3}\) \(\left[-\left(-\frac{1}{3}\right)^2.9+1\right]\) = \(\frac{1}{3}\) \(\left(-\frac{1}{9}.9+1\right)\) = \(\frac{1}{3}\) (-1+1) = \(\frac{0}{3}\) = 0
d)= \(\left(15\frac{1}{4}-25\frac{1}{4}\right)\): \(\left(-\frac{5}{7}\right)\) = (-10) : \(\left(-\frac{5}{7}\right)\) = 14
bài 97 :
a) = -6,37 . ( 0,4 . 2,5 ) = -6,37 . 1 = -6,37
b) = ( - 0,125 . 8 ) . (-5,3) = (-1) . (-5,3) = 5,3
c) = [ ( -2,5 ) . (-4) ] . (-7,9) = 10 . ( -7,9) = -79
d) = [ ( -0,375 ) . (-8) ] . \(\frac{13}{3}\) = 3.\(\frac{13}{3}\) = 13
bài 98 :
a) => y = \(\frac{21}{10}\) :\(\left(-\frac{3}{5}\right)\) => y = \(-\frac{7}{2}\)
b) => y = \(-\frac{64}{33}.\frac{3}{8}=-\frac{8}{11}\)
c) => \(\frac{7}{5}y\) = \(-\frac{4}{5}-\frac{3}{7}\) => \(\frac{7}{5}y\) = \(-\frac{43}{35}\) => y = \(-\frac{43}{35}:\frac{7}{5}\) = \(-\frac{43}{49}\)
d) => \(-\frac{11}{12}y=\frac{5}{6}-\frac{1}{4}\Rightarrow-\frac{11}{12}y=\frac{7}{12}\Rightarrow y=-\frac{7}{11}\)
bài 103 :
gọi a , b là tiền lãi mà mỗi tổ chức được chia ( a, b \(\in\) Z*) ta có :
\(\frac{a}{3}=\frac{b}{5}\) và a+b = 12800000
Từ \(\frac{a}{3}=\frac{b}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau :
\(\Rightarrow\frac{a}{3}=\frac{b}{5}=\frac{a+b}{3+5}=\frac{12800000}{8}=1600000\)
vậy \(\frac{a}{3}=1600000\Rightarrow a=4800000\)
\(\frac{b}{5}=1600000\Rightarrow b=8000000\)
( thỏa mãn điều kiện )
Tiền lãi mà các tổ chức đã được chia là 4800000 đồng và 8000000 đồng
bài 104 :
sau khi bán , tấm thứ 1 còn \(\frac{1}{2}\) , tấm thứ 2 còn \(\frac{1}{3}\) , tấm thứ 3 còn \(\frac{1}{4}\)
Gọi chiều dài các tấm theo thứ tự là x, y , z ( x,y,z \(\in\) Z* ) , ta có :
\(\frac{1}{2}x=\frac{1}{3}y=\frac{1}{4}z\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+y+z}{2+3+4}=\frac{108}{9}=12\)
Vậy \(\frac{x}{2}=12\Rightarrow x=24\left(m\right)\)
\(\frac{y}{3}=12\Rightarrow y=36\left(m\right)\)
\(\frac{z}{4}=12\Rightarrow z=48\left(m\right)\)
( thỏa mãn điều kiện )
Chiều dài mỗi tấm vải lúc bạn đầu lần lượt là 24(m) , 36(m) , 48(m)
bài 105 :
a) ta có \(\sqrt{0,01}=0,1;\sqrt{0,25}=0,5\)
vậy \(\sqrt{0,01}-\sqrt{0,25}=0,1-0,5=-0,4\)
b) \(\sqrt{100}=10\Rightarrow0,5\sqrt{100}=0,5.10=5\)
\(\sqrt{\frac{1}{4}}=\sqrt{0,25}=0,5\)
vậy \(0,5\sqrt{100}-\sqrt{\frac{1}{4}}=5-0,5=4,5\)
~~Chúc bạn học tốt

Giải:
∆AHB và ∆KBH có
AH=KH ( gt )
=
BH cạnh chung .
Nên ∆AHB=∆KBH(c.g.c)
Suy ra: =
Vậy BH là tia phân giác của góc B.
Tương tự ∆AHC =∆KHC ( c . g . c )
Suy ra: =
Vậy CH là tia phân giác của góc C
p/s: Very làm biếng open sách so copy mạng =]]]

Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=>
hay DK là phân giác
=> =
∆ADI = ∆BDI (c.c.c)
=>
=> DI là phân giác
=> =
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay + = 900
Do đó + = 900
=> + = 1800
Xem thêm tại: http://loigiaihay.com/bai-55-trang-80-sgk-toan-lop-7-tap-2-c42a5841.html#ixzz44NZ9vg5o

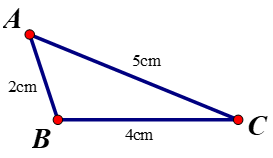
Dựa vào hình vẽ, ta có:
Góc đối diện cạnh BC là Â
Góc đối diện cạnh AC là B̂
Góc đối diện cạnh AB là Ĉ
Mà: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm ⇒ AB < BC < CA ⇒ Ĉ < Â < B̂.
2)heo định lý tổng ba góc trong tam giác ABC, ta có:
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
Kiến thức áp dụng
+ Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
+ Định lý tổng ba góc trong tam giác: Trong một tam giác, tổng ba góc bằng 180º.
3 a) Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.
b) Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có
4) Trong một tam giác ta luôn có:
+ Góc đối diện với cạnh lớn hơn là góc lớn hơn
⇒ góc đối diện với cạnh nhỏ nhất là góc nhỏ nhất.
+ Góc nhỏ nhất luôn là góc nhọn.
(Giả sử tồn tại tam giác có góc nhỏ nhất không phải góc nhọn
⇒ Góc nhỏ nhất ≥ 90º ⇒ cả ba góc ≥ 90º ⇒ tổng ba góc trong tam giác ≥ 90º.3 = 270º.
5) + Trong ∆BCD có góc C tù (gt) nên góc C lớn nhất ⇒ BD lớn nhất (vì BD là cạnh đối diện với góc C) ⇒ BD > CD (1).
+ Áp dụng định lý góc ngoài trong tam giác BCD ta có :
nên góc ABD cũng là góc tù.
Trong ∆ABD có góc B tù (cmt) nên góc B lớn nhất ⇒ AD lớn nhất (vì AD là cạnh đối diện với góc B) ⇒ AD > BD
(2).
Từ (1) và (2) suy ra AD > BD > CD.
Vậy Hạnh đi xa nhất, Trang đi gần nhất.
6)Vì D nằm giữa A và C (giả thiết)
⇒ AC = AD + DC = AD + BC (DC = BC theo đề bài)
⇒ AC > BC
Mà trong tam giác ABC :
Góc đối diện cạnh AC là góc B
Góc đối diện cạnh BC là góc A
Ta lại có: AC > BC (cmt)
⇒ B̂ > Â (theo định lí 1)
Hay  < B̂.
Vậy kết luận c) là đúng.
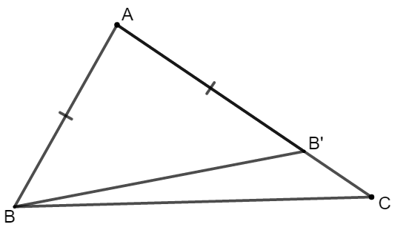
7)
a) Trên tia AC, ta có : AC > AB mà AB = AB’ ⇒ AC > AB’ ⇒ B’ nằm giữa A và C.
⇒ tia B’B nằm giữa hai tia BA và BC.
b) ∆ABB’ có AB = AB’ nên ∆ABB’ cân tại A.
c) Vì góc AB'B là góc ngoài tại B’ của ∆BB’C

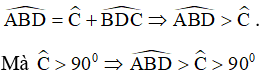
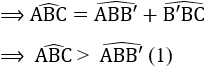
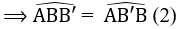
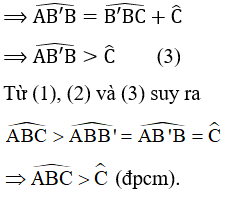
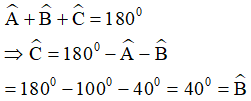
Biết d song2 với d' thì => góc A1 = góc B3 và:
b) góc A1 = góc B4 và
c) góc A1+ B2=180 độ
a) Nếu 1 đường thẳng cắt 2 đường thẳng song2 thì:
a) 2 góc so le trong bằng nhau
b) 2 góc đồng vị bằng nhau
c) 2 góc trong cùng phía bù nhau
Biết : (hình 25b)
a) góc A4 = góc B2
hoặc b) góc A1 = góc B1
hoặc c) góc A1 + B2 = 180 độ
thì suy ra d song2 với d'
Nếu 1 đường thẳng cắt 2 đường thẳng
mà a) 2 góc so le trong bằng nhau
hoặc b) 2 góc đồng vị bằng nhau
hoặc c) 2 góc trong cùng phía bù nhau thì 2 đường thẳng đó song2 với nhau.