K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 8 2021
Bài 4:
d: Ta có: \(x^2-y^2-2x-2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)
e: Ta có: \(x^3-y^3-3x+3y\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-3\right)\)
DA
4
20 tháng 8 2021
2.
\(a,x^4-y^4=\left(x^2-y^2\right)\left(x^2+y^2\right)=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\)
\(b,x^2-3y^2=\left(x-y\sqrt{3}\right)\left(x+y\sqrt{3}\right)\)
\(c,\left(3x-2y\right)^2-\left(2x-3y\right)^2\\ =\left(3x-2y-2x+3y\right)\left(3x-2y+2x-3y\right)\\ =\left(x+y\right)\left(5x-5y\right)=5\left(x-y\right)\left(x+y\right)\)
\(d,9\left(x-y\right)^2-4\left(x+y\right)^2\\ =\left[3\left(x-y\right)-2\left(x+y\right)\right]\left[3\left(x-y\right)+2\left(x+y\right)\right]\\ =\left(3x-3y-2x-2y\right)\left(3x-3y+2x+2y\right)\\ =\left(x-5y\right)\left(5x-y\right)\)
\(e,\left(4x^2-4x+1\right)-\left(x+1\right)^2\\ =\left(2x-1\right)^2-\left(x+1\right)^2\\ =\left(2x-1-x-1\right)\left(2x-1+x+1\right)\\ =3x\left(x-2\right)\)
\(f,x^3+27=\left(x+3\right)\left(x^2+3x+9\right)\)
\(g,27x^3-0,001=\left(3x-0,1\right)\left(9x^2+0,027x+0,01\right)\)
\(h,125x^3-1=\left(5x-1\right)\left(25x^2+5x+1\right)\)
20 tháng 8 2021
Bài 3 :
a) \(x^4+2x^2+1=\left(x^2+1\right)^2\)
b) \(4x^2-12xy+9y^2=\left(2x-3y\right)^2\)
c) \(-x^2-2xy-y^2=-\left(x+y\right)^2\)
e) \(\left(x+y\right)^2-2\left(x+y\right)+1=\left(x+y-1\right)^2\)
f) \(x^3-3x^2+3x-1=\left(x-1\right)^3\)
g) \(x^3+6x^2+12x+8=\left(x+2\right)^3\)
h) \(x^3+1-x^2-x=\left(x+1\right)\left(x^2-x+1\right)-x\left(x+1\right)=\left(x+1\right)\left(x^2-2x+1\right)=\left(x+1\right)\left(x-1\right)^2\)
l) \(\left(x+y\right)^2-x^3-y^3=\left(x+y\right)^3-\left(x+y\right)\left(x^2-xy+y^2\right)=\left(x+y\right)\left(x^2+2xy+y^2-x^2+xy-y^2\right)=3xy\left(x+y\right)\)
NT
0
T
0
17 tháng 1 2023
Bài 3:
a: Xét ΔABC có AE/AB=AF/AC
nên EF//BC và EF=1/2BC=7,5cm
\(AC=\sqrt{15^2-9^2}=12\left(cm\right)\)
S=1/2*9*12=54cm2
b: Xét ΔCAB có CF/CA=CH/CB
nên FH//AB và FH=AB/2
=>FH//AE và FH=AE
=>AEHF là hình bình hành
mà góc FAE=90 độ
nên AEHF là hình chữ nhật
CÁC BẠN GIÚP MÌNH VS Ạ MÌNH ĐANG CẦN GẤP Ạ
17 tháng 9 2021
Gọi E là giao điểm của AC và BD.
∆ECD có ∠C1 = ∠D1 (do ∠ACD = ∠BDC) nên là tam giác cân.
Suy ra EC = ED (1)
Tương tự ∆EAB cân tại A suy ra: EA = EB (2)
Từ (1) và (2) ta có: EA + EC = EB + ED ⇒ AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.4
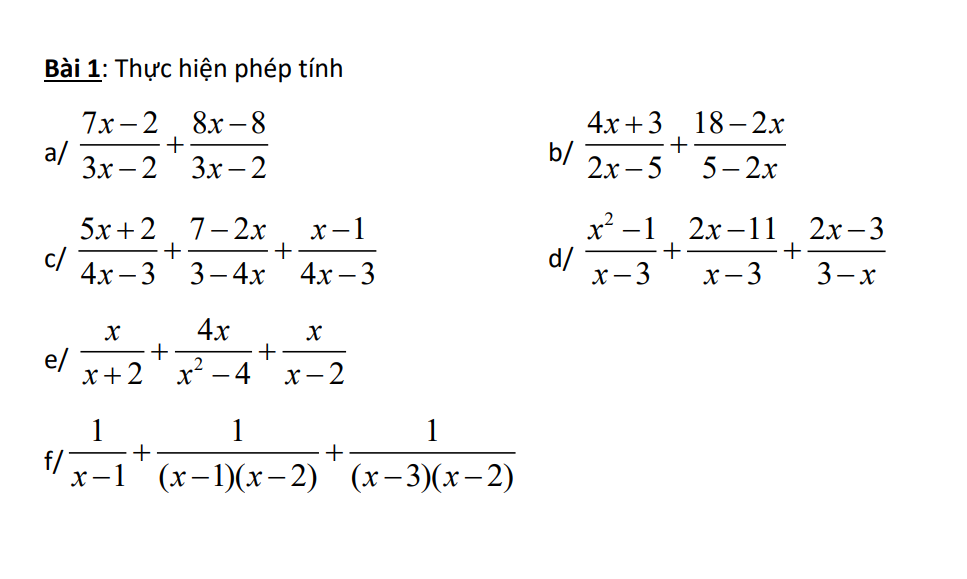
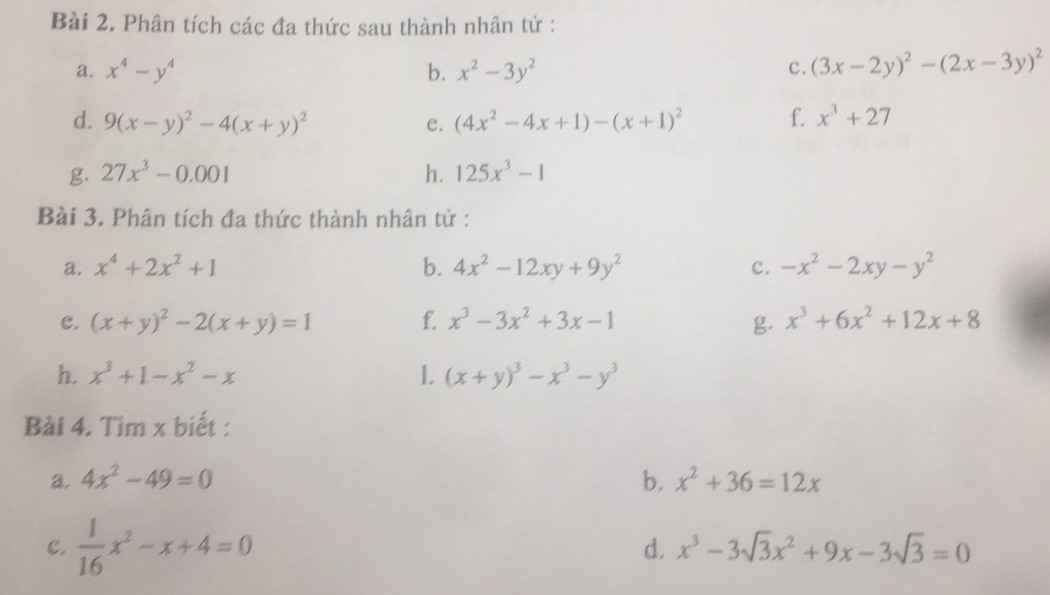
\(a,=\dfrac{7x-2+8x-8}{3x-2}=\dfrac{5\left(3x-2\right)}{3x-2}=5\\ b,=\dfrac{4x+3+2x-18}{2x-5}=\dfrac{3\left(2x-5\right)}{2x-5}=3\\ c,=\dfrac{5x+2+2x-7+x-1}{4x-3}=\dfrac{2\left(4x-3\right)}{4x-3}=2\\ d,=\dfrac{x^2-1+2x-11+3-2x}{x-3}=\dfrac{\left(x-3\right)\left(x+3\right)}{x-3}=x+3\\ e,=\dfrac{x^2-2x+4x+x^2+2x}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x}{x-2}\)
\(f,=\dfrac{x^2-5x+6+x-3+x-1}{\left(x-1\right)\left(x-2\right)\left(x-3\right)}=\dfrac{\left(x-1\right)\left(x-2\right)}{\left(x-1\right)\left(x-2\right)\left(x-3\right)}=\dfrac{1}{x-3}\)