K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 3 2022
Nửa chu vi hình chữ nhật:14 cm
Gọi chiều dài hình chữ nhật là x (cm) với \(7< x< 14\)
Chiều rộng hình chữ nhật là: \(14-x\) (cm)
Diện tích ban đầu của hình chữ nhật: \(x\left(14-x\right)\)
Chiều dài hình chữ nhật sau khi tăng 1cm: \(x+1\)
Chiều rộng sau khi tăng 2cm: \(14-x+2=16-x\)
Diện tích lúc sau: \(\left(x+1\right)\left(16-x\right)\)
Do diện tích tăng lên 25 \(cm^2\) nên ta có pt:
\(\left(x+1\right)\left(16-x\right)-x\left(14-x\right)=25\)
\(\Leftrightarrow x+16=25\)
\(\Leftrightarrow x=9\left(cm\right)\)
Vậy hình chữ nhật ban đầu dài 9cm và rộng 5cm
TB
0
27 tháng 10 2021
Bài 4:
a) áp dụng pi-ta-go ta có:\(AB^2+AC^2=BC^2\Rightarrow BC=\sqrt{15^2+20^2}=25\)
áp dụng HTL ta có: \(AB.AC=BC.AH\Rightarrow\dfrac{15.20}{25}=AH\Rightarrow AH=12\)
b) áp dụng HTL và ΔAHB ta có: \(AI.AB=AH^2\)
áp dụng HTL và ΔAHC ta có: \(AJ.AC=AH^2\)
\(\Rightarrow AI.AB=AJ.AC\)
TH
0
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 6 2021
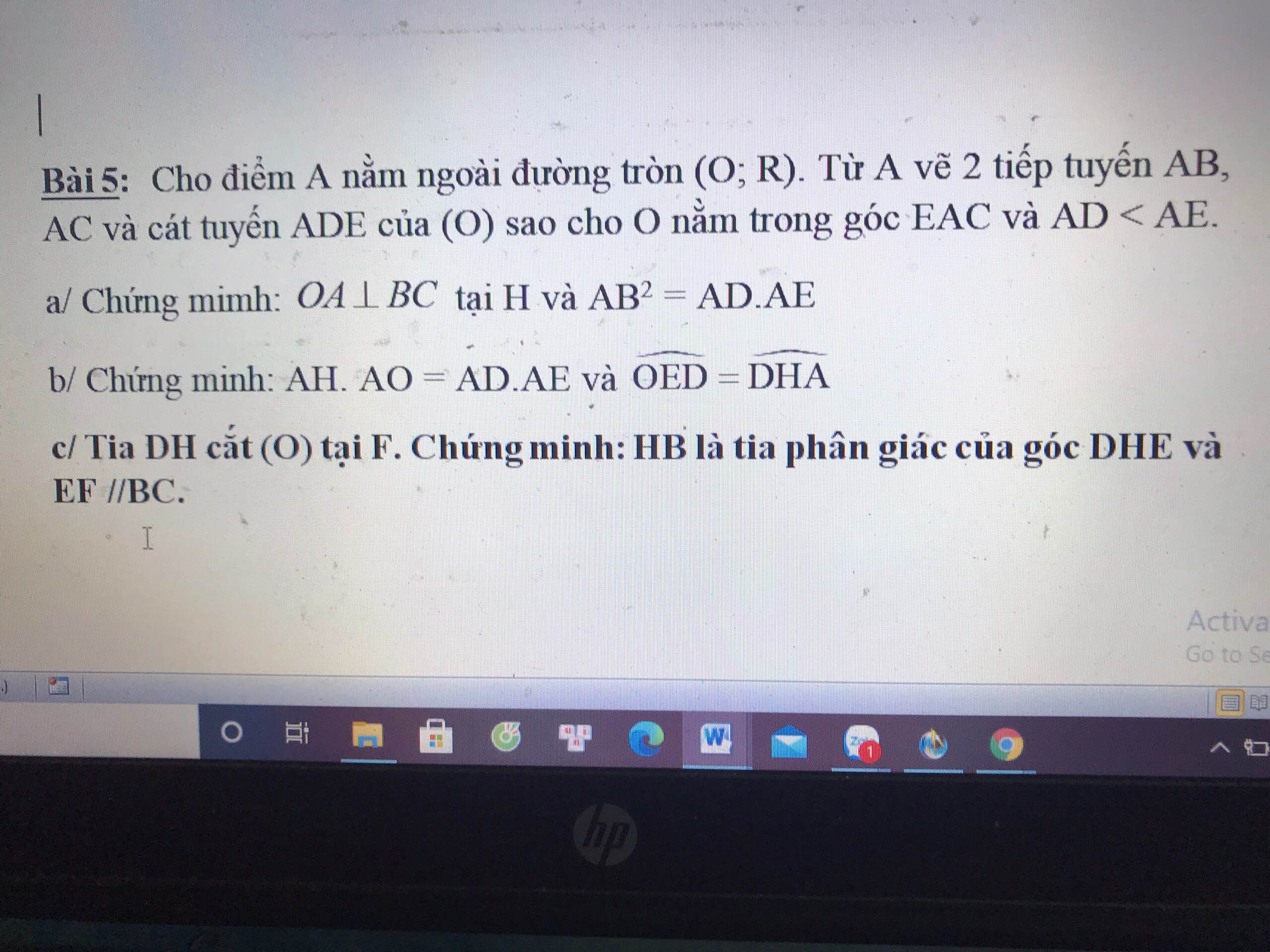
AB là tiếp tuyến nên \(AB\perp OB\) hay tam giác OAB vuông tại B
Áp dụng hệ thức lượng trong tam giác OAB với đường cao BH:
\(AB^2=AH.AO\)
Mà theo câu a. ta có \(AB^2=AD.AE\)
\(\Rightarrow AH.AO=AD.AE\)
//Từ đó ta cũng suy ra \(\dfrac{AH}{AD}=\dfrac{AE}{AO}\)
Xét hai tam giác AHE và ADO có: \(\left\{{}\begin{matrix}\dfrac{AH}{AD}=\dfrac{AE}{AO}\\\widehat{OAE}-chung\end{matrix}\right.\)
\(\Rightarrow\Delta AHE\sim\Delta ADO\left(c.g.c\right)\)
\(\Rightarrow\widehat{DOA}=\widehat{HEA}\)
\(\Rightarrow\) Tứ giác OHDE nội tiếp (2 góc cùng chắn DH bằng nhau)
\(\Rightarrow\widehat{OED}+\widehat{OHD}=180^0\)
Mà \(\widehat{OHD}+\widehat{DHA}=180^0\)
\(\Rightarrow\widehat{OED}=\widehat{DHA}\)
22 tháng 9 2021
Đề ko rõ ràng \(\sqrt{x^2}+x+\dfrac{1}{4}\) hay \(\sqrt{x^2+x+\dfrac{1}{4}}\)??
3 tháng 10 2021
\(A=\left(4x^2+2\cdot2\cdot\dfrac{1}{4}x+\dfrac{1}{16}\right)-\dfrac{1}{16}=\left(2x+\dfrac{1}{4}\right)^2-\dfrac{1}{16}\ge-\dfrac{1}{16}\\ A_{min}=-\dfrac{1}{16}\Leftrightarrow2x+\dfrac{1}{4}=0\Leftrightarrow x=-\dfrac{1}{8}\)
Câu 40: C