Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

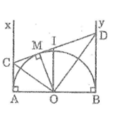
Chu vi hình thang ABDC bằng: AB + 2CD (chứng minh trên)
Suy ra: 14 = 4 + 2.CD ⇒ CD = 5 (cm)
Hay CM + DM = 5 ⇒ DM = 5 – CM (1)
Tam giác COD vuông tại O có OM ⊥ CD
Theo hệ thức lượng trong tam giác vuông, ta có:
O M 2 = CM.DM ⇔ 2 2 = CM.DM ⇔ 4 = CM.DM (2)
Thay (1) vào (2) ta có: CM.(5 – CM) = 4
⇔ 5CM – C M 2 – 4 = 0 ⇔ 4CM – C M 2 + CM – 4 = 0
⇔ CM(4 – CM) + (CM – 4) = 0 ⇔ CM(4 – CM) – (4 – CM) = 0
⇔ (CM – 1)(4 – CM) = 0 ⇔ CM – 1 = 0 hoặc 4 – CM = 0
⇔ CM = 1 hoặc CM = 4
Vì CM = CA (chứng minh trên) nên AC = 1 (cm) hoặc AC = 4 (cm)
Vậy điểm C cách điểm A 1cm hoặc 4cm thì hình thang ABDC có chu vi bằng 14.

Bài này nhớ hôm trước làm rồi mà không nhớ ở câu nào nữa == , ngại tìm lại nên làm luôn :>
a) Ta có : OC , OD là các tia phân giác của 2 góc kề bù nên \(\widehat{COD}=90^o\) . Gọi I là trung điểm của CD tì :
IC = ID = IO
nên I là tâm và IO là bán kính của đường tròn có đường kính CD
b)
Chu vi hình thang ABDC bằng :
AB + AC + BD + CD
Ta dễ dàng chứng inh được :
AC + BD = CM + MD = CD
nên chu vi ABDC bằng AB + 2CD
Ta có AB không đổi nên chu vi ABDC nhỏ nhất và bằng 3AB .
c)
Đặt AC = x ; BD = y . Chu vi ABCD bằng :
AB + 2CD = 4 + 2( x + y )
Do chu vi ABDC bằng 14 nên :
4 + 2( x + y ) = 14
hay
x + y = 5 (1)
Ta lại có :
xy = MC . MD
= OM2 ( hệ thức lượng tam giác vuông COD )
nên xy = 22 = 4 (2)
Từ (1) , (2) suy ra :
\(x+\frac{4}{x}=5\Leftrightarrow x^2+4=5x\Leftrightarrow x^2-5x+4=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-4\right)=0\Leftrightarrow x=1;4\)
Vậy , nếu điểm C ( thuộc tia Ax ) cách điểm A là 1 cm hoặc 4 cm thì chu vi hình thang ABDC vẫn bằng 14cm

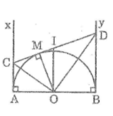
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC
Suy ra: OI // AC ⇒ OI ⊥ AB
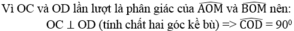
Suy ra: IC = ID = IO = (1/2).CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD. Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.

bài làm
a, gọi H là tiếp điểm của tiếp tuyến MN
theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
nên ta có: MN=HM=HN=\(\dfrac{1}{2}\)(AOH =HON)=90 độ
vậy góc MON=90 đọ và là tâm giác vuông tại O đường cao OH
b,theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
Theo hệ thức lượng trong tam giác vuông:
Vì vậy =\(R^2\)

cho tam giác ABC vuông tại A. Vẽ các đường tròn O và i đi qua A và tiếp xúc với BC tại các điểm B và C. Gọi M là trung điểm của BC. Chứng Minh
a) Các đường tròn O và i tiếp xúc với nhau
b) AM là tiếp tuyến chung của hai đường tròn O và i
c) tam giác OMI vuông
d) BC là tiếp tuyến của đường tròn ngoại tiếp tam giác OMI.

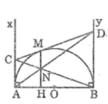
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Trong tam giác BND, ta có AC // BD
Suy ra: ND/NA = BD/AC (hệ quả định lí Ta-lét) (1)
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = CM và BD = DM (2)
Từ (1) và (2) suy ra: ND/NA = MD/MC
Trong tam giác ACD, ta có: ND/NA = MD/MC
Suy ra: MN // AC (theo định lí đảo định lí Ta-lét)
Mà: AC ⊥ AB (vì Ax ⊥ AB)
Suy ra: MN ⊥ AB


Theo tính chất hai tiếp tuyến cắt nhau ta có:
CA = CM
DB = DM
Suy ra: AC + BD = CM + DM = CD
Chu vi hình thang ABDC bằng: AB + BD + DC + CA = AB + 2CD
Vì đường kính AB của (O) không thay đổi nên chu vi hình thang nhỏ nhất khi CD nhỏ nhất
Ta có: CD ≥ AB nên CD nhỏ nhât khi và chỉ khi CD = AB
Khi đó CD // AB ⇔ OM ⊥ AB
Vậy khi M là giao điểm của đường thẳng vuông góc với AB tại O với nửa đường tròn (O) thì hình thang ABDC có chu vi nhỏ nhất.