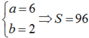Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
![]()
![]()
Ta có ![]()
Phương trình đã cho thành ![]()
đây là phương trình đẳng cấp, ta có thể chia cả hai vế cho b > 0 như sau:

+) TH1. ![]()

+) TH2. 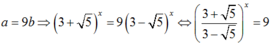

Do đó 

Chọn C.
Điều kiện: 5x – 1 > 0 hay x > 0
Phương trình đã cho tương đương:
log2( 5x - 1) [log2( 5x - 1) + 1] = 2
Đặt t = log2(5x - 1), khi đó phuơng trình trở thành: t(t + 1) = 2
Suy ra t = 1 hoặc t = -2
Với t =1 ta có log2(5x - 1) = 1 nên 5x – 1 = 2; x = log53
Với t = -2ta có log2(5x - 1) = - 2 nên 5x – 1 = 2-2; x = log5(5/4)
Mặt khác x1 > x2 suy ra 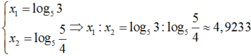

Đáp án B
P T ⇔ log 2 2 x 2 - x + 2 m - 4 m 2 + log 2 x 2 + m x - 2 m 2 = 0
⇔ 2 x 2 - x + 2 m - 4 m 2 = x 2 + m x - 2 m 2 > 0
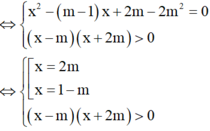
Điều kiện để pt đã cho có 2 nghiệm
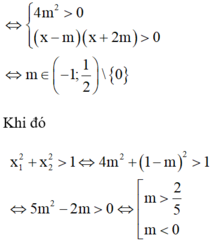
Do đó
S = - 1 ; 0 ∪ 2 5 ; 1 2 ⇒ A = - 1 + 2 + 1 = 2

ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)
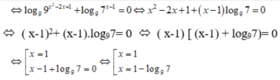

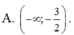
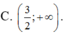
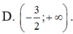
Chọn B.
Phương trình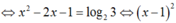
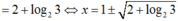
Do đó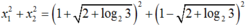
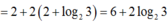
Từ đó: