
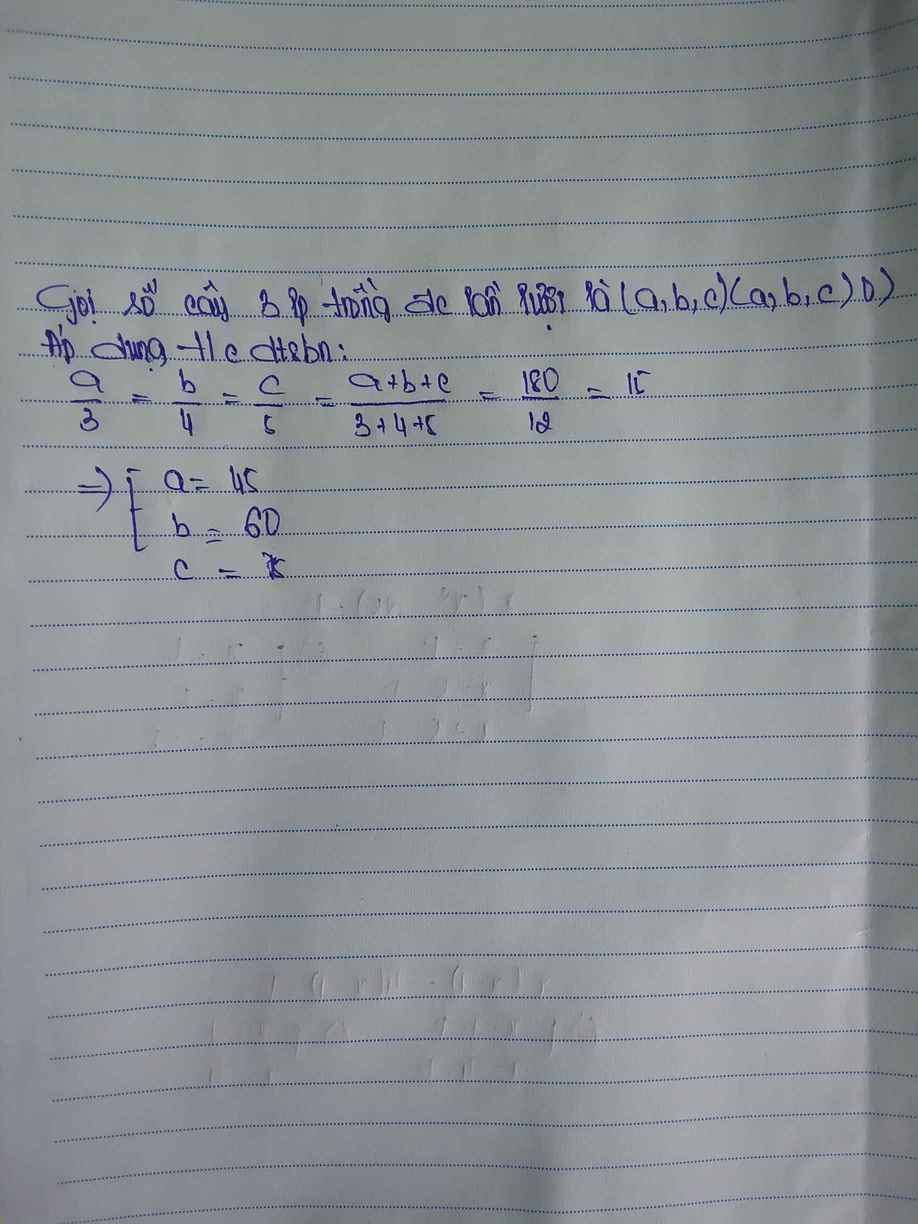
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

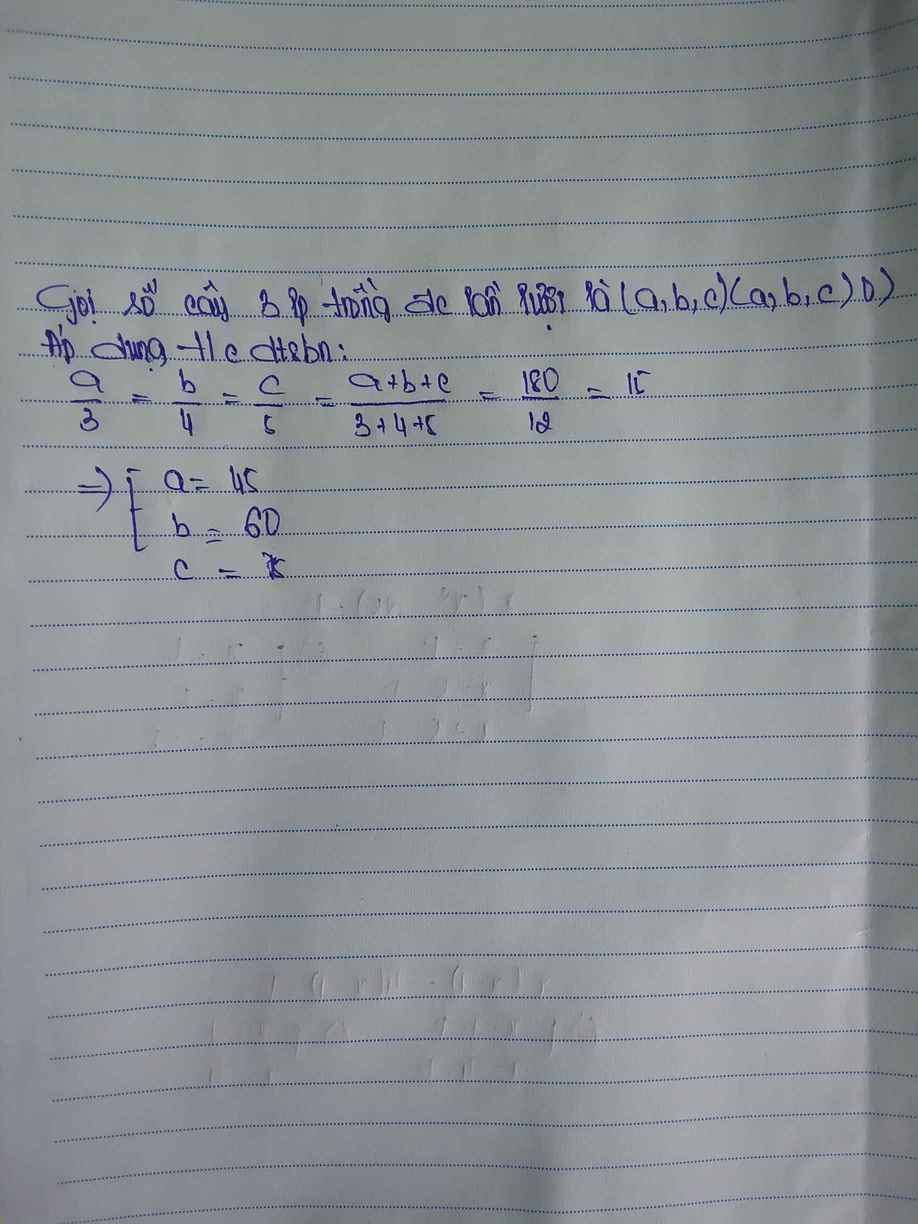

Lớp 7A : 45
Lớp 7B : 60
Lớp 7C : 75
Có cần giải thích không bạn

gọi số cây của lớp 7A; 7B; 7C lần lượt là a; b; c (cây; a,c,b > 0)
ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
\(\Rightarrow\frac{a+b+c}{3+4+5}=\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{180}{12}\)
\(\Rightarrow\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=15\)
\(\Rightarrow\hept{\begin{cases}a=15\cdot3=45\\b=15\cdot4=60\\c=15\cdot5=75\end{cases}}\)
Để cho tiện,ta gọi số cây của ba lớp trên lần lượt là: 7A,7B,7C
Theo đề bài,ta có: \(\frac{7A}{3}=\frac{7B}{4}=\frac{7C}{5}\)và \(7A+7B+7C=180\)
Áp dụng t/c dãy tỉ số bằng nhau ta có: \(\frac{7A}{3}=\frac{7B}{4}=\frac{7C}{5}=\frac{7A+7B+7C}{3+4+5}=\frac{180}{12}=15\)
Từ: \(\frac{7A}{3}=15\Rightarrow7A=15.3=45\)cây
\(\frac{7B}{4}=15\Rightarrow7B=15.4=60\) cây
\(\frac{7C}{5}=15\Rightarrow7C=75\) cây

gọi số cây 3 lớp 7a. 7b, 7c trồng được lần lượt là : a; b; c (a; b; c thuộc N*; cây)
số cây của 3 lớp 7a; 7b; 7c lần lượt tỉ lệ với 3; 4; 5
=> a/3 = b/4 = c/5
=> (a+b+c)/(4+5+6) = a/3 = b/4 = c/5
mà 3 lớp trồng đươc 180 cây => a + b + c = 180
=> 180/15 = a/3 = b/4 = c/5
=> 16 = a/3 = b/4 = c/5
=> a = 16.3 = 48
b = 16.4= 64
c = 16.5 = 80
Gọi số cây trồng của lớp 7A,7B,7C lần lượt là x,y,z ( x,y,z \(\in\)N* ; x,y,z < 180 )
Theo đề bài ta có : x : y : z = 3 : 4 : 5 hay \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)hay x + y + z = 180
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{180}{12}=15\)
=> \(\hept{\begin{cases}\frac{x}{3}=15\\\frac{y}{4}=15\\\frac{z}{5}=15\end{cases}}\)=> \(\hept{\begin{cases}x=45\\y=60\\z=75\end{cases}}\)

\(\text{Gọi số cây mà 3 lớp 7A,7A,7C trồng được lần lượt là a,b,c }\)
\(\text{Theo bài ra, ta có:}\)
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}\text{ và a+b+c=150}\)
\(\text{Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :}\)
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{a+b+c}{4+5+6}=\frac{150}{15}=10\)
\(\Rightarrow a=50;b=60;c=70\)
\(\text{Vậy 3 lớp 7A,7B,7C lần lượt trồng được 40,50,60 cây}\)
Gọi a, b, c lần lượt là số cây lớp 7A, 7B, 7C trồng được (a, b, c > 0 )
Vì \(a:b:c=4:5:6\Leftrightarrow\frac{a}{4}=\frac{b}{5}=\frac{c}{6}\)và a+ b + c = 150
Theo tính chất dãy tỉ số bằng nhau
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{a+b+c}{4+5+6}=\frac{150}{15}=10\)
\(\hept{\begin{cases}\frac{a}{4}=10\Rightarrow a=40\\\frac{b}{5}=10\Rightarrow b=50\\\frac{c}{6}=10\Rightarrow c=60\end{cases}}\)
vậy.....

2. Gọi số hs tiên tiến của lớp 7A,7B,7C lần lượt là a,b,c(hs)(a,b,c∈N*)
Ta có \(a:b:c=5:4:3\Rightarrow\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{c}{3}\) và \(a-b=3\left(hs\right)\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{a-c}{5-4}=\dfrac{3}{1}=3\\ \Rightarrow\left\{{}\begin{matrix}a=15\\b=12\\c=9\end{matrix}\right.\)
Vậy ...
1. Gọi số cây trồng được của lớp 7A,7B,7C lần lượt là a,b,c(cây)(a,b,c∈N*)
Ta có \(a:b:c=3:4:5\Rightarrow\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{120}{12}=10\\ \Rightarrow\left\{{}\begin{matrix}a=30\\b=40\\c=50\end{matrix}\right.\)
Vậy ...

gọi x;y;z lần lượt là số cây 3 lớp 7A;7B;7C
theo đề ta có: \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)và x+y+z=180
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{180}{12}=15\)
suy ra: \(\frac{x}{3}=15\Rightarrow x=3.15=45\)
\(\frac{y}{4}=15\Rightarrow y=4.15=60\)
\(\frac{z}{5}=15\Rightarrow z=15.5=75\)
vậy số cây 3 lớp 7A;7B;7C lần lượt là : 45;60;75

Giải:
Gọi số cây lớp 7a,7b,7c trồng được lần lượt là a,b,c (a,b,c\(\in\)N)
Theo bài ra ta có: \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)và a+b+c=180
Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{180}{12}=15\)
+) \(\frac{a}{3}=15\Rightarrow a=45\)
+) \(\frac{b}{4}=15\Rightarrow b=60\)
+) \(\frac{c}{5}=15\Rightarrow c=75\)
Vậy lớp 7a trồng được 45 cây
lớp 7b trồng được 60 cây
lớp 7c trồng được 75 cây

Gọi x,y,z (cây) lần lượt là số cây trồng được của ba lớp 7A, 7B và 7C ( x, y, z \(\in\) N*)
Do số cây trồng được của ba lớp 7A,7B,7C lần lượt tỉ lệ với 6 ; 4 ; 5 nên:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{5}\)
Do tổng số cây của lớp 7B và 7C trồng được nhiều hơn của lớp 7A là 15 cây nên:
\(y+z-x=15\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{y+z-x}{4+5-6}=\dfrac{15}{3}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=5\cdot6=30\\y=5\cdot4=20\\z=5\cdot5=25\end{matrix}\right.\)
Vậy ...
#Đạt Đang Bận Thở
Gọi số cay trồng được của lớp 7A,7B,7C lần lượt là a,b,c
Theo đề, ta có: a/6=b/4=c/5
Áp dụng tính chất của DTSBN, ta được:
a/6=b/4=c/5=(a-c)/(6-5)=15
=>a=90; b=60; c=75