Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\\left(SAB\right)\cap\left(ABCD\right)=AB\\SA\perp AB\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(\widehat{SBA}=45^0\) (do SAB vuông cân tại A)
b.
\(\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=AB\sqrt{2}=2a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{SC}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SCA}\approx35^015'\)

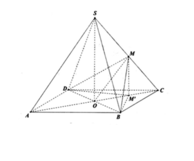
Do S.ABCD là chóp đều \(\Rightarrow BD\perp\left(SAC\right)\)
Mà BD là giao tuyến (MBD) và (ABCD)
\(\Rightarrow\widehat{MOC}\) là góc giữa (MBD) và (ABCD)
\(OC=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\) ; \(MC=OM=\dfrac{1}{2}SC=\dfrac{a}{2}\)
Áp dụng định lý hàm cosin:
\(cos\widehat{MOC}=\dfrac{OM^2+OC^2-CM^2}{2OM.OC}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{MOC}=45^0\)

a: Xét ΔBAC có BA=BC và góc ABC=60 độ
nên ΔABC đều
=>\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
=>\(S_{ABCD}=\dfrac{a^2\sqrt{3}}{2}\)
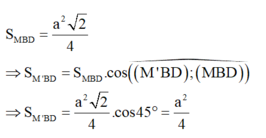

Đề bài thiếu dữ liệu định vị điểm S (ví dụ SC bằng bao nhiêu đó) nên ko thể tính góc giữa SB và (ABCD)