
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu này mình sót +3x ở sau cùng vế phải. Không hiểu vì sao đánh rồi mà lại bị mất

Xét \(I_1=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)cosxdx=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)d\left(sinx\right)\)
Đặt \(sinx=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=5-t\)
\(I_1=2\int\limits^1_0\left(5-t\right)dt=9\)
Xết \(I_2=3\int\limits^1_0f\left(3-2x\right)dx=-\dfrac{3}{2}\int\limits^1_0f\left(3-2x\right)d\left(3-2x\right)\)
Đặt \(3-2x=t\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(t\right)=t^2+3\)
\(I_2=-\dfrac{3}{2}\int\limits^1_3\left(t^2+3\right)dt=\dfrac{3}{2}\int\limits^3_1\left(t^2+3\right)dt=22\)
\(\Rightarrow I=9+22=31\)

Mặt cầu tâm \(I\left(1;1;0\right)\) bán kính \(R=5\)
\(\Rightarrow IA=\sqrt{6^2+8^2}=10=2R\)
Gọi C là trung điểm IA \(\Rightarrow C\left(4;5;0\right)\Rightarrow IC=R=5\Rightarrow C\in\left(S\right)\)
Gọi D là trung điểm IC \(\Rightarrow D\left(\dfrac{5}{2};3;0\right)\), đồng thời do D là trung điểm IC \(\Rightarrow MD\perp IC\) và IM=IC=R hay tam giác MDF vuông tại D
Lại có: \(CM=CA=CI=R\Rightarrow\) tam giác AMI vuông tại M
\(\Rightarrow\Delta_VMID\sim\Delta_VAIM\) (chung góc I)
\(\Rightarrow\dfrac{MA}{MD}=\dfrac{AI}{AM}=\dfrac{2R}{R}=2\Rightarrow MA=2MD\)
\(\Rightarrow P=MA+2MB=2MD+2MB=2\left(MD+MB\right)\ge2DB=2\sqrt{\left(\dfrac{5}{2}\right)^2+\left(3-8\right)^2+0^2}=5\sqrt{5}\)


4.
a.
- Với \(m=0\Rightarrow y=-1\) hàm không có tiệm cận
- Với \(m\ne0\)
\(\lim\limits_{x\rightarrow\infty}\dfrac{x-1}{mx^2-x+1}=0\Rightarrow y=0\) là tiệm cận ngang
Xét phương trình \(mx^2-x+1=0\) có \(\Delta=1-4m\)
+ Với \(m>\dfrac{1}{4}\Rightarrow\Delta< 0\Rightarrow\) \(mx^2-x+1=0\) vô nghiệm hay ĐTHS ko có tiệm cận đứng
+ Với \(m=\dfrac{1}{4}\Rightarrow mx^2-x+1=0\) có nghiệm kép hay ĐTHS có 1 tiệm cận đứng
+ Với \(m< \dfrac{1}{4}\Rightarrow mx^2-x+1=0\) có 2 nghiệm pb (và luôn khác 1 với \(m\ne0\) ) nên ĐTHS có 2 tiệm cận đứng.
Kết luận...
4b.
- Với \(m=0\Rightarrow\lim\limits_{x\rightarrow\infty}\dfrac{-1}{x^2-x-2}=0\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow\left\{-1;2\right\}}\dfrac{-1}{x^2-x-2}=\infty\) nên \(x=-1;x=2\) là 2 tiệm cận đứng
- Với \(m\ne0\)
\(\lim\limits_{x\rightarrow\infty}\dfrac{mx^3-1}{x^2-x-2}=\infty\) nên ĐTHS không có tiệm cận ngang
Phương trình \(x^2-x-2=0\) có 2 nghiệm \(x=\left\{-1;2\right\}\) nên:
+ Nếu \(m=-1\Rightarrow-x^3-1=0\) có 1 nghiệm \(x=-1\Rightarrow\) hàm có đúng 1 tiệm cận đứng \(x=2\)
+ Nếu \(m=\dfrac{1}{8}\Rightarrow\dfrac{1}{8}x^3-1=0\) có 1 nghiệm \(x=2\Rightarrow\) ĐTHS hàm có đúng 1 tiệm cận đứng \(x=-1\)
+ Nếu \(m\ne\left\{-1;\dfrac{1}{8}\right\}\Rightarrow mx^3-1=0\) có nghiệm khác \(\left\{-1;2\right\}\Rightarrow\) ĐTHS có 2 tiệm cận đứng.
Kết luận...

1.
a.
ĐKXĐ: \(x^2-1>0\Rightarrow\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\)
\(log_2\left(x^2-1\right)=3\)
\(\Rightarrow x^2-1=8\)
\(\Leftrightarrow x^2=9\)
\(\Rightarrow x=\pm3\) (tm)
b.
ĐKXĐ: \(x>0\)
\(log_3x+log_{\sqrt{3}}x+log_{\dfrac{1}{3}}x=6\)
\(\Leftrightarrow log_3x+2log_3x-log_3x=6\)
\(\Leftrightarrow log_3x=3\)
\(\Rightarrow x=3^3=27\)
c. ĐKXĐ: \(x>0\)
\(log_{\sqrt{2}}^2x+3log_2x+log_{\dfrac{1}{2}}x=2\)
\(\Leftrightarrow\left(2log_2x\right)^2+3log_2x-log_2x=2\)
\(\Leftrightarrow4log_2^2x+2log_2x-2=0\)
\(\Rightarrow\left[{}\begin{matrix}log_2x=-1\\log_2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\sqrt{2}\end{matrix}\right.\)

Ta có: (u.v)' = u'.v + u.v'
\(Q=80K^{\dfrac{1}{3}}\left(100-K\right)^{\dfrac{1}{2}}\)
\(Q'=80.\left(K^{\dfrac{1}{3}}\right)'.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\left(\left(100-K\right)^{\dfrac{1}{2}}\right)'\)= \(80.\dfrac{1}{3}.K^{-\dfrac{2}{3}}.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\dfrac{1}{2}.\left(100-K\right)^{-\dfrac{1}{2}}.\left(-1\right)\) = \(80.\left(\dfrac{\left(100-K\right)^{\dfrac{1}{2}}}{3K^{\dfrac{2}{3}}}-\dfrac{K^{\dfrac{1}{3}}}{2\left(100-K\right)^{\dfrac{1}{2}}}\right)\)= \(80.\left(\dfrac{2\left(100-K\right)^{\dfrac{1}{2}}\left(100-K\right)^{\dfrac{1}{2}}-3K^{\dfrac{2}{3}}K^{\dfrac{1}{3}}}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{2\left(100-K\right)-3K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{200-5K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(\dfrac{400\left(40-K\right)}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\) = \(\dfrac{200\left(40-K\right)}{3K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\).
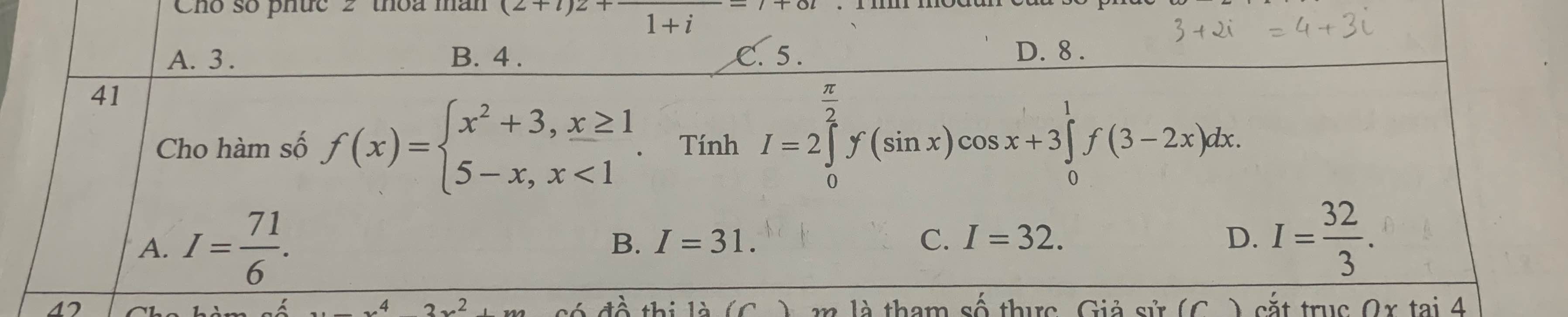

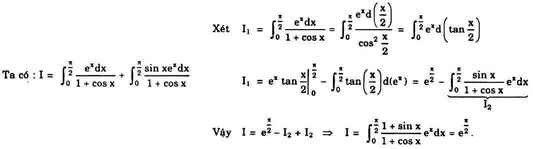





Đáp án:
1 + 1 = 2
= 2 nha
CHÚC BẠN HỌC TỐT