Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn phương làm đúng rùi, sao k tisk cho bn ấy, mk tisk cho bn

\(A=\left(\dfrac{x}{x+2}+\dfrac{8x+8}{x^2+2x}-\dfrac{x+2}{x}\right):\left(\dfrac{x^2-x-3}{x^2+2x}+\dfrac{1}{x}\right)\)
\(\Leftrightarrow A=\left(\dfrac{x^2}{x\left(x+2\right)}+\dfrac{8x+8}{x\left(x+2\right)}-\dfrac{\left(x+2\right)^2}{x\left(x+2\right)}\right):\left(\dfrac{x^2-x-3}{x\left(x+2\right)}+\dfrac{x+2}{x\left(x+2\right)}\right)\)
\(\Leftrightarrow A=\dfrac{x^2+8x+8-\left(x+2\right)^2}{x\left(x+2\right)}:\dfrac{x^2-x-3+x+2}{x\left(x+2\right)}\)
\(\Leftrightarrow A=\dfrac{x^2+8x+8-x^2-4x-4}{x\left(x+2\right)}:\dfrac{x^2-1}{x\left(x+2\right)}\)
\(\Leftrightarrow A=\dfrac{4x+4}{x\left(x+2\right)}.\dfrac{x\left(x+2\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow A=\dfrac{4\left(x+1\right)}{x\left(x+2\right)}.\dfrac{x\left(x+2\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow A=\dfrac{4}{x-1}\)
\(A=\dfrac{x^2+8x+8-x^2-4x-4}{x\left(x+2\right)}:\dfrac{x^2-x-3+x^2+2x}{x\left(x+2\right)}\)
\(=\dfrac{4\left(x+1\right)}{x-3}\)

a: Xét tứ giác MNQP có
I là trung điểm của NP
I là trung điểm của MQ
Do đó: MNQP là hình bình hành
mà MQ=NP
nên MNQP là hình chữ nhật

\(\dfrac{x}{12}+\dfrac{1}{4}=\dfrac{x}{10}\)
\(\leftrightarrow\)\(\dfrac{5x}{60}+\dfrac{15}{60}=\dfrac{6x}{60}\)
\(\leftrightarrow\)\(5x+15=6x\)
\(\leftrightarrow\)\(15=6x-5x\)
\(\leftrightarrow\)\(15=x\)

c) \(=\left(4x-3\right)^2-\left(9x^2-4\right)\)
\(=16x^2-24x+9-9x^2+4=7x^2-24x+13\)
d) \(=\left(x^2-3x+2\right)\left(x+3\right)-\left(x^3-5x^2\right)\)
\(=x^3+3x^2-3x^2-9x+2x+6-x^3+5x^2\)
\(=5x^2-7x+6\)
c. (4x - 3)(4x - 3) - (3x + 2)(3x - 2)
= (4x - 3)2 - (9x2 - 4)
= 16x2 - 24x + 9 - 9x2 + 4
= 16x2 - 9x2 - 24x + 9 + 4
= 7x2 - 24x + 13
d. (x - 2)(x - 1)(x + 3) - x2(x - 5)
= (x2 - 1 - 2x + 2)(x + 3) - x2(x - 5)
= x3 + 3x2 - x - 3 - 2x2 - 6x + 2x + 6 - x3 + 5
= x3 - x3 + 3x2 - 2x2 - x - 6x + 2x + 6 + 5 - 3
= x2 - 5x + 8

Câu 1:
a)2x-3=5
\(\leftrightarrow\)2x=5+3
\(\leftrightarrow\)2x=8
\(\leftrightarrow\)x=4
Vậy pt có tập nghiệm S={4}
b)(2x+1)(x-3)=0
\(\leftrightarrow\) 2x+1=0
Hoặc x-3=0
\(\leftrightarrow\)x=-1/2
x=3
Vậy pt có tập nghiệm S={-1/2;3}
d)3x-4=11
\(\leftrightarrow\)3x=11+4
\(\leftrightarrow\)3x=15
\(\leftrightarrow\)x=5
Vậy pt có tập nghiệm S={5}
e)(2x-3)(x+2)=0
\(\leftrightarrow\)2x-3=0
Hoặc x+2=0
\(\leftrightarrow\)x=3/2
hoặc x=-2
Vậy pt có tập nghiệm S={3/2;-2}
Câu 2:
a)2x-3<15
\(\leftrightarrow\)2x<15+3
\(\leftrightarrow\)2x<18
\(\leftrightarrow\)x<9
Vật bpt có tập nghiệm S={x|x<9}
c)5x-2<18
\(\leftrightarrow\)5x<20
\(\leftrightarrow\)x<4
Vậy bpt có tập nghiệm S={x|x<4}
Mấy bài phân số nhác gõ quá~

Bạn tự vẽ hình nhé!
a, Xét \(\Delta ABC.và.\Delta ABH.có:\)
\(\widehat{BAC}=\widehat{BHA}\)
\(\widehat{B}.chung\)
\(\Rightarrow\Delta ABC\sim\Delta ABH\)
b, Áp dụng định lý Pytago vào tam giác vuông ABC, ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=4^2+5^2=41\\ \Rightarrow BC=\sqrt{41}\approx6,4\left(cm\right)\)
Vì \(\Delta ABC\sim\Delta ABH\) và \(\Delta ABC\) có đường cao AH:
\(\Rightarrow\dfrac{BH}{BA}=\dfrac{HC}{AC}\) ( 1 )
Dựa vào tính chất dãy tỉ số bằng nhau, ta lại có:
\(\left(1\right)\Rightarrow\dfrac{BH}{BA}=\dfrac{HC}{AC}=\dfrac{BH+HC}{BA+AC}=\dfrac{BC}{4+5}=\dfrac{6,4}{9}\)
\(\Rightarrow BH=\dfrac{4.6,4}{9}=2,8\left(cm\right)\)
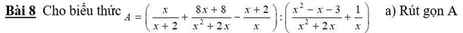





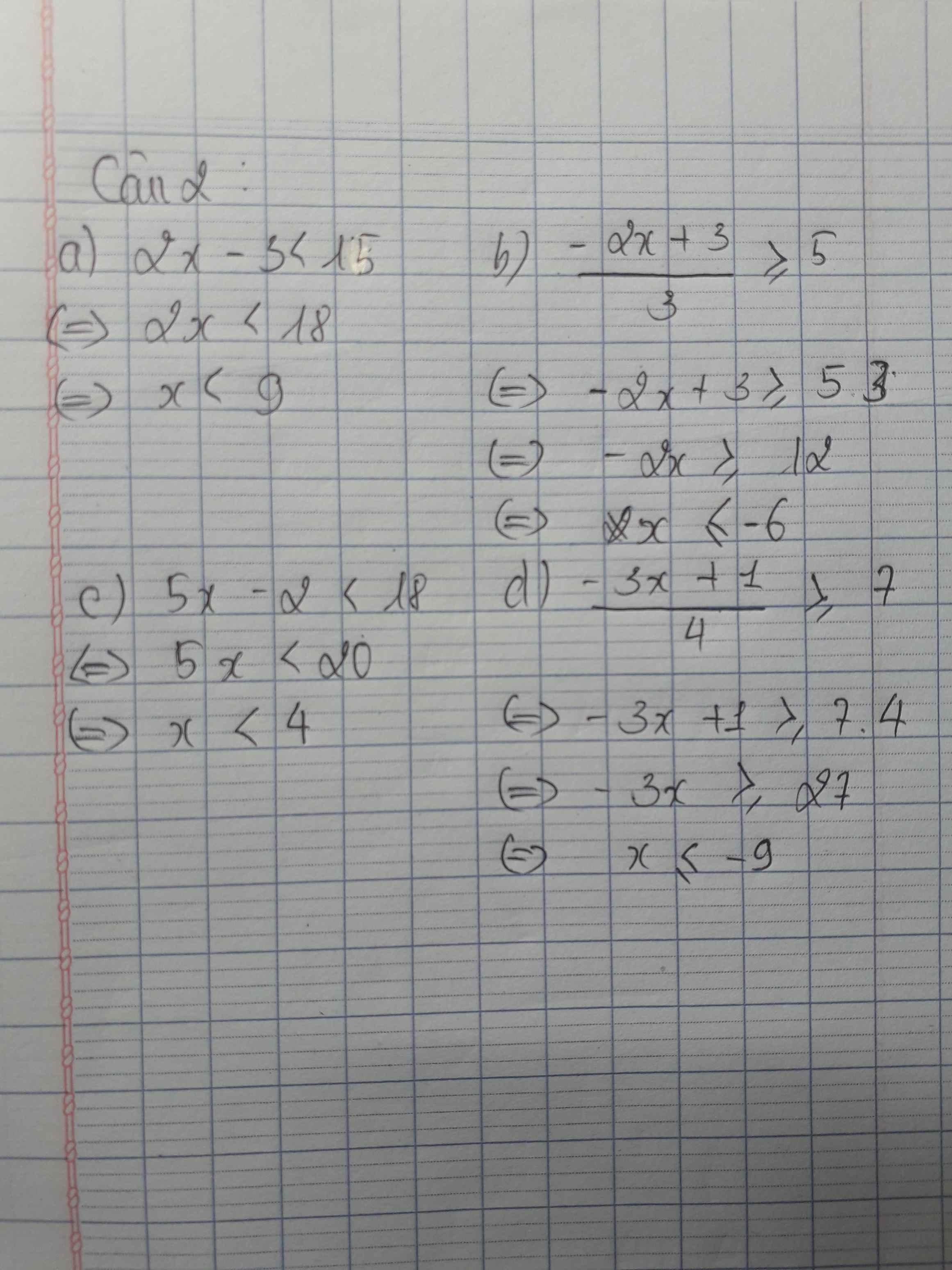
herlp, hẻlp