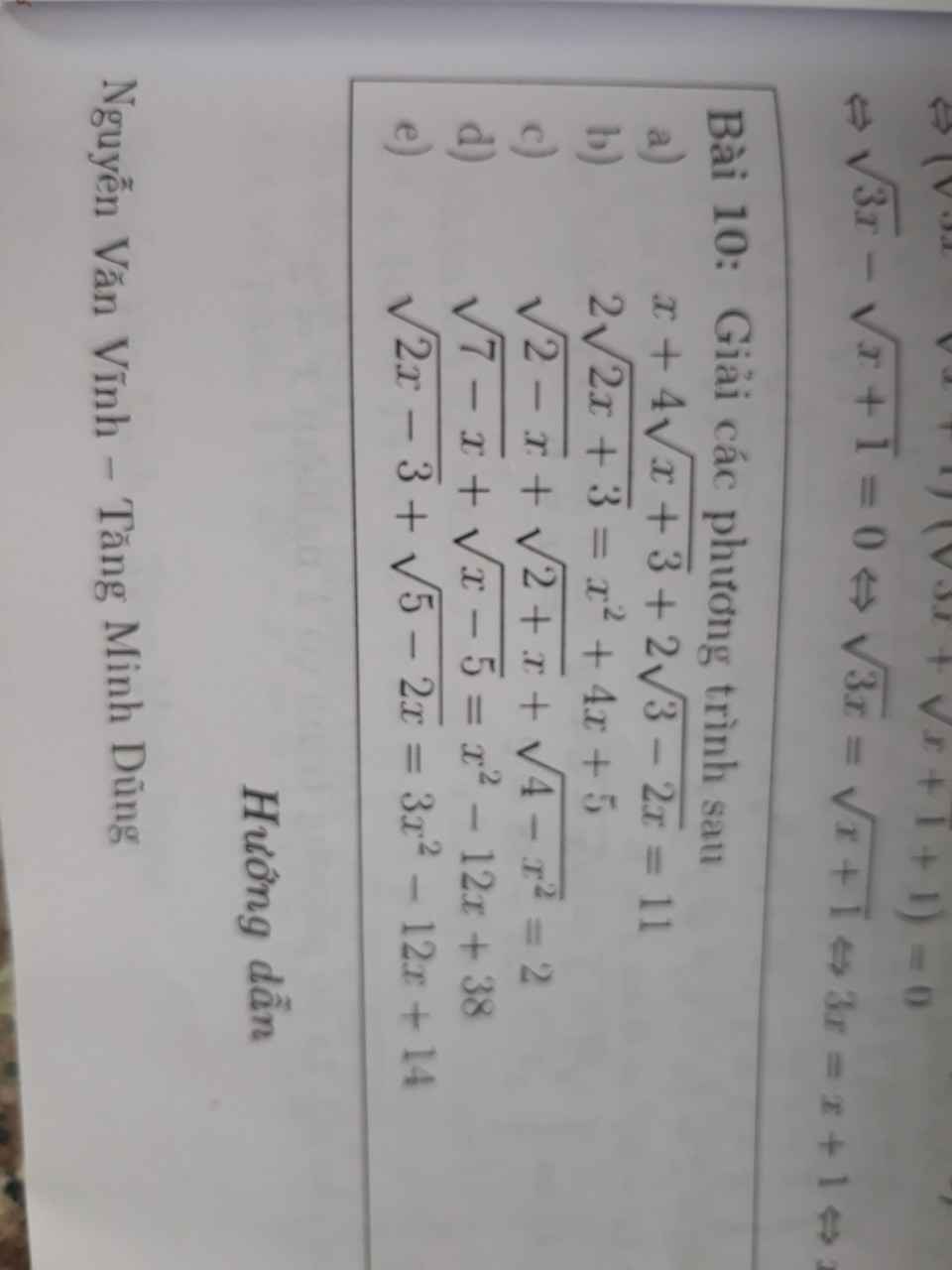K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KN
0
2 tháng 12 2021
\(1,\left\{{}\begin{matrix}3x-y=5\\5x+2y=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\5x+2\left(3x-5\right)=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\5x+6x-10=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\11x=33\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3.3-5\\x=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)
\(2,\left\{{}\begin{matrix}5x-4y=3\\2x+y=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x-4\left(4-2x\right)=3\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x-16+8x=3\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}13x=19\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{13}\\y=4-2.\dfrac{19}{13}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{13}\\y=\dfrac{14}{13}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
a.
ĐKXĐ: \(-3\le x\le\dfrac{3}{2}\)
Ta có:
\(4\sqrt{x+3}=2.2\sqrt{x+3}\le2^2+x+3=x+7\)
\(2\sqrt{3-2x}=2.1.\sqrt{3-2x}\le1^2+3-2x=4-2x\)
Do đó:
\(x+4\sqrt{x+3}+2\sqrt{3-2x}\le x+x+7+4-2x=11\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\sqrt{x+3}=2\\\sqrt{3-2x}=1\end{matrix}\right.\) \(\Leftrightarrow x=1\)
Vậy pt có nghiệm duy nhất \(x=1\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
b.
ĐKXĐ: \(x\ge-\dfrac{3}{2}\)
\(x^2+4x+5-2\sqrt{2x+3}=0\)
\(\Leftrightarrow\left(x^2+2x+1\right)+\left(2x+3-2\sqrt{2x+3}+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2+\left(\sqrt{2x+3}-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=0\\\sqrt{2x+3}-1=0\end{matrix}\right.\)
\(\Leftrightarrow x=-1\)
Vậy pt có nghiệm duy nhất \(x=-1\)
20 tháng 9 2021
Bài là tam giác vuông hả bạn?
Ta có : BC = BH + CH = \(\sqrt{2}+\sqrt{8}=3\sqrt{2}\)
Xét △ ABC vuông tại A, đường cao AH có:
\(AB^2\)=BH.BC ( hệ thức lượng trong tam giác vuông)
=> \(AB^2=\sqrt{2}.3\sqrt{2}=6\)
=> \(AB=\sqrt{6}\)
\(AC^2=BC.HC\)
=> \(AC^2=\sqrt{8}.3\sqrt{2}=12\)
=>\(AC=2\sqrt{3}\)
\(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.\sqrt{6}.2\sqrt{6}=3\sqrt{2}\left(cm^2\right)\)
