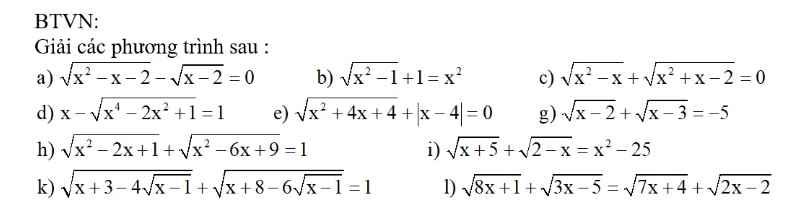K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
1
17 tháng 10 2021
\(4,\\ b,B=\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{x}\ge3\sqrt[3]{\dfrac{xyz}{xyz}}=3\)
Dấu \("="\Leftrightarrow x=y=z\)
\(c,x+y=4\Leftrightarrow x=4-y\\ \Leftrightarrow C=\left(4-y\right)^2+y^2\\ C=16-8y+y^2+y^2=2\left(y^2-4y+4\right)+8\\ C=2\left(y-2\right)^2+8\ge8\\ C_{min}=8\Leftrightarrow x=y=2\)
NQ
0
A
1
12 tháng 12 2021
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
NL
1
17 tháng 10 2021
Bài 7:
a: \(A=x+\sqrt{x}\ge0\forall x\)
Dấu '=' xảy ra khi x=0
NL
0
KN
0
NL
1
5 tháng 11 2021
Bài 5:
a: Xét ΔBEC và ΔADC có
\(\widehat{C}\) chung
\(\widehat{EBC}=\widehat{DAC}\)
Do đó: ΔBEC\(\sim\)ΔADC
NL
3
20 tháng 10 2021
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\le-1\\x\ge2\end{matrix}\right.\)
\(\sqrt{x^2-x-2}-\sqrt{x-2}=0\\ \Leftrightarrow\sqrt{x^2-x-2}=\sqrt{x-2}\\ \Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=2\left(tm\right)\end{matrix}\right.\)
20 tháng 10 2021
\(a,ĐK:x\ge2\\ PT\Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=2\\ b,ĐK:\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-1}=x^2-1\\ \Leftrightarrow x^2-1=\left(x^2-1\right)^2\\ \Leftrightarrow\left(x^2-1\right)\left(x^2-1-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-1\left(tm\right)\\x=\sqrt{2}\left(tm\right)\\x=-\sqrt{2}\left(tm\right)\end{matrix}\right.\)
\(c,ĐK:\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-x}=-\sqrt{x^2+x-2}\\ \Leftrightarrow x^2-x=x^2+x-2\\ \Leftrightarrow2x=2\\ \Leftrightarrow x=1\left(tm\right)\)
