K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 11 2021
Câu 2:
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=1\\4a+b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=3\\a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=1-a=2\end{matrix}\right.\)
HP
6 tháng 5 2021
2.
\(x^2+2x+m+1\le0\)
\(\Leftrightarrow m\le f\left(x\right)=-\left(x+1\right)^2\)
Yêu cầu bài toán thỏa mãn khi:
\(\Leftrightarrow m\le maxf\left(x\right)=max\left\{f\left(-1\right);f\left(3\right)\right\}=0\)
Vậy \(m\le0\)
HP
6 tháng 5 2021
3.
\(f\left(x\right)=x^2-2mx-3m\le0\)
Yêu cầu bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}\Delta'\ge0\\f\left(-1\right)\le0\\f\left(3\right)\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2+3m\ge0\\1-m\le0\\-9m-9\le0\end{matrix}\right.\Leftrightarrow m\ge1\)
Vậy \(m\ge1\)
nhìu quá
NT
1
21 tháng 6 2023
Cái này bạn quy đồng lên thôi
\(\dfrac{pi}{3}+\dfrac{kpi}{3}=\dfrac{2pi}{6}+\dfrac{k2pi}{6}=\dfrac{k2pi+2pi}{6}=\dfrac{\left(k+1\right)\cdot2pi}{6}\)
Do là k2pi và (k+1)2pi là hai điểm trùng nhau nên được tính chung luôn là k2pi bạn nha
5 tháng 11 2021
Bài 6:
b: PTHĐGĐ là:
\(x^2+4x-1=x-3\)
\(\Leftrightarrow x^2+3x-4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=-7\\y=-2\end{matrix}\right.\)
8 tháng 6 2021
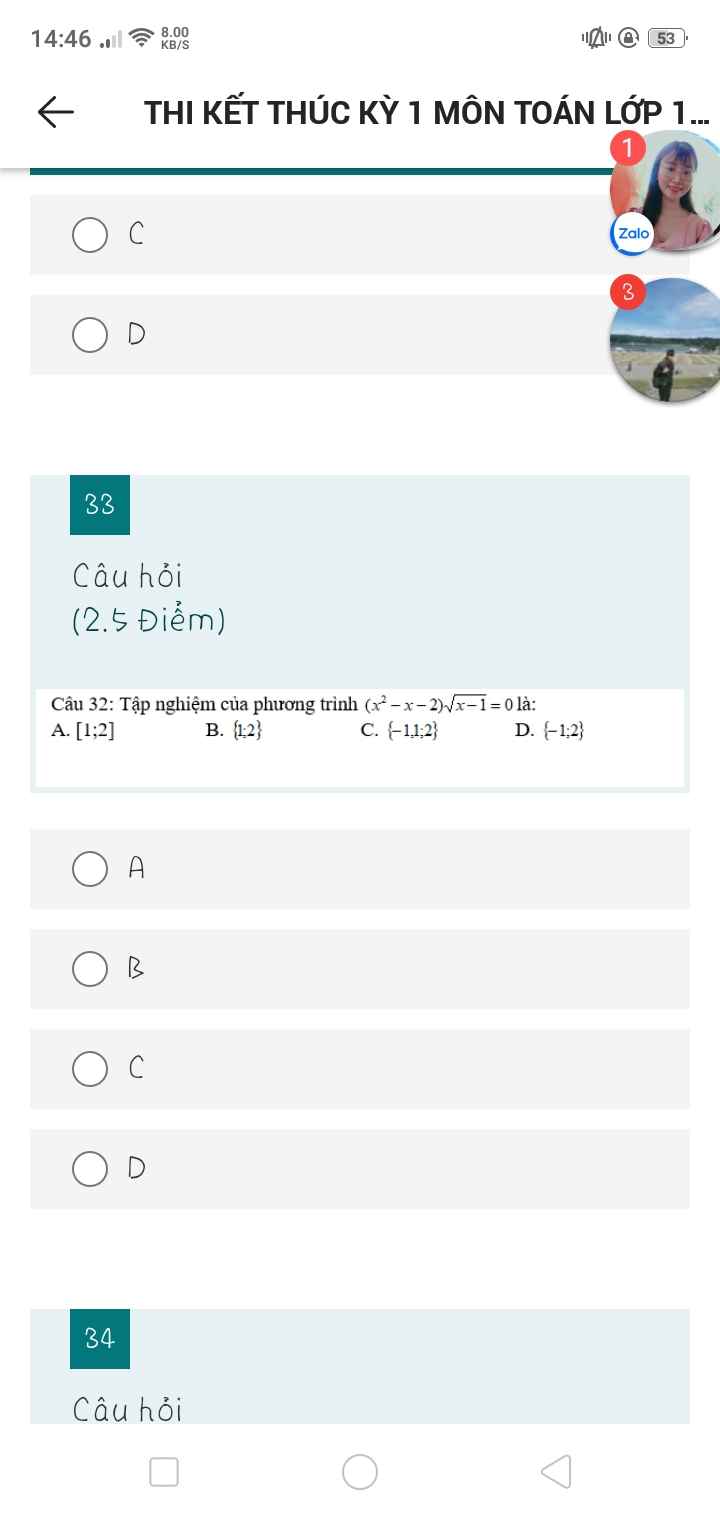
\(\left(x^2-x-2\right)\sqrt{x-1}=0\left(đk:x\ge1\right)\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\) (do x+1>0)
Ý B.
