K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Giải bài giúp em vs ạ em cần gấp lắm cảm ơn
16 tháng 9 2021
a)\(A=\left\{2,3,4,5\right\}\)
b)\(B=\left\{-2,-1,0,1,2\right\}\)
c)\(C=\left\{-3;0;3;6;9\right\}\)
d)\(A=\left\{3;4;7;12;19\right\}\)
16 tháng 9 2021
a)\(n\in\)\(N^*\); \(3< n^2< 30\Leftrightarrow\sqrt{3}< n< \sqrt{30}\)
\(\Rightarrow n=\left\{2;3;4;5\right\}\)
\(\Rightarrow A=\left\{2;3;4;5\right\}\)
b)\(\left|n\right|< 3\Leftrightarrow-3< n< 3\) mà \(n\in Z\)
\(\Rightarrow n=\left\{-2;-1;0;1;2\right\}\)
\(\Rightarrow B=\left\{-2;-1;0;1;2\right\}\)
c)Các phần tử của C là x ; x=3k với k nguyên và thỏa mãn \(-4< x< 12\)
\(\Rightarrow x=\left\{-3;0;3;6;9\right\}\) (với các k lần lượt là \(-1;0;1;2;3\))
\(\Rightarrow C=\left\{-3;0;3;6;9\right\}\)
d)Các phần tử của A có dạng \(n^2+3\) với \(n\in N;n< 5\Rightarrow n=\left\{0;1;2;3;4\right\}\)
\(\Rightarrow A=\left\{3;4;7;12;19\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
a.
\(0< a< \dfrac{\pi}{2}\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\) ; \(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
\(\Rightarrow A=\dfrac{\dfrac{4}{3}+\dfrac{3}{4}}{\dfrac{4}{3}-\dfrac{3}{4}}=...\)
b.
\(A=\dfrac{\dfrac{2sina}{cosa}+\dfrac{3cosa}{cosa}}{\dfrac{4sina}{cosa}-\dfrac{5cosa}{cosa}}=\dfrac{2tana+3}{4tana-5}=\dfrac{2.3+3}{4.3-5}=...\)
\(B=\dfrac{\dfrac{3sina}{cos^3a}-\dfrac{2cosa}{cos^3a}}{\dfrac{5sin^3a}{cos^3a}+\dfrac{4cos^3a}{cos^3a}}=\dfrac{3tana\left(1+tan^2a\right)-2\left(1+tan^2a\right)}{5tan^3a+4}=...\) em tự thay số
c.
\(B=\dfrac{cos^2x+2sinx.cosx+1}{sin^2x+3}=\dfrac{\dfrac{cos^2x}{cos^2x}+\dfrac{2sinx.cosx}{cos^2x}+\dfrac{1}{cos^2x}}{\dfrac{sin^2x}{cos^2x}+\dfrac{3}{cos^2x}}\)
\(=\dfrac{1+2tanx+\left(1+tan^2x\right)}{tan^2x+3\left(1+tan^2x\right)}=...\)
6 tháng 2 2023
Bài 1:
a: Đặt 14,4-3,6t^2=0
=>3,6t^2=14,4
=>t^2=4
=>t=2
b: TXĐ: [0;2]
TGT: [0;14,4]
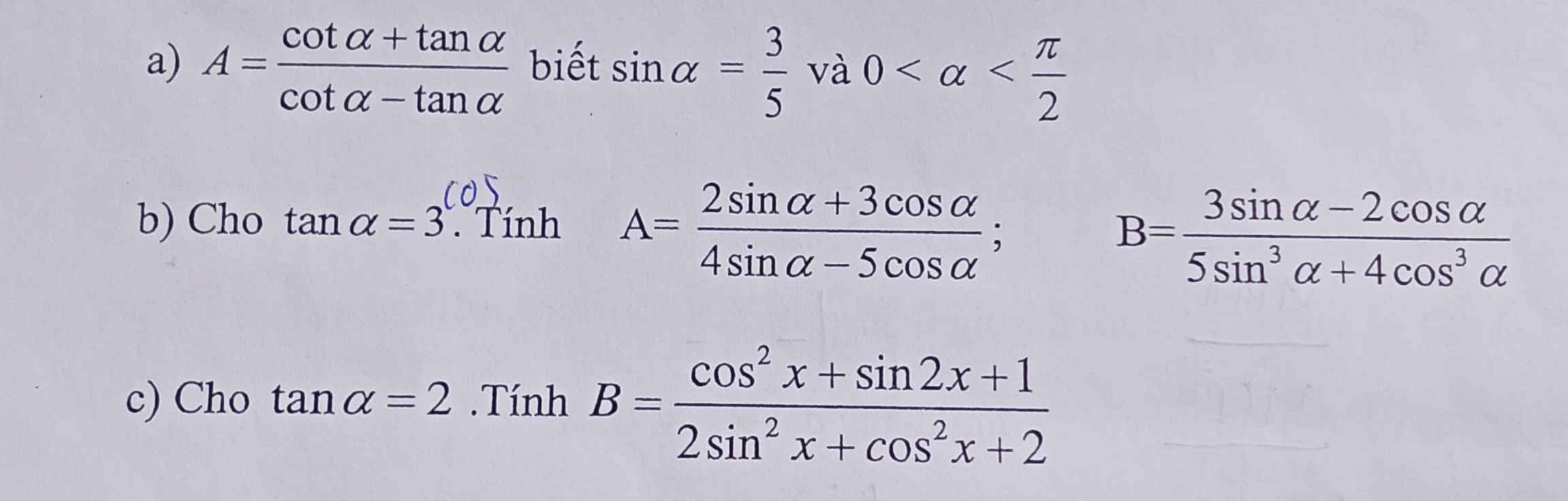
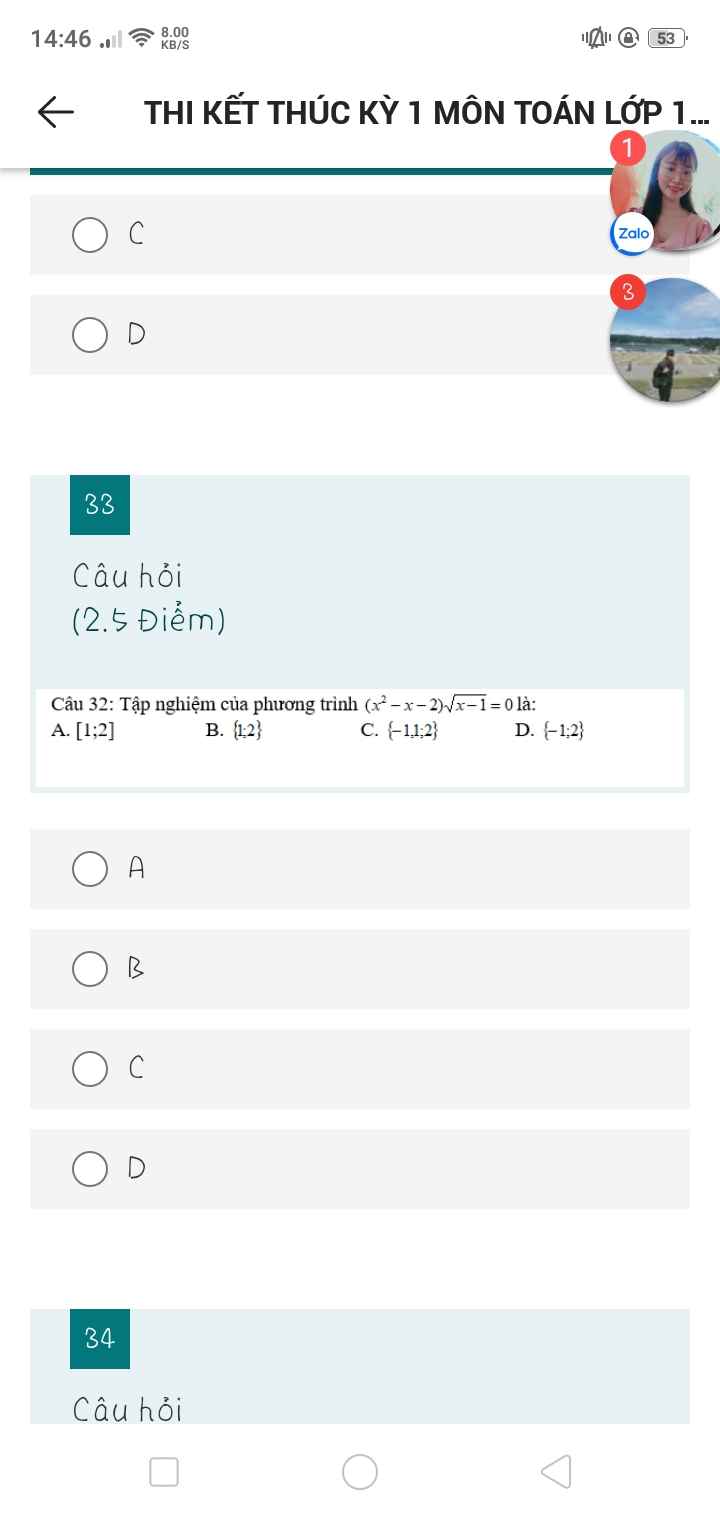
\(\left(x^2-x-2\right)\sqrt{x-1}=0\left(đk:x\ge1\right)\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\) (do x+1>0)
Ý B.
B