Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+9^2=117\)
hay \(BC=3\sqrt{13}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AB\cdot AC=AH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{12\sqrt{13}}{13}\left(cm\right)\\CH=\dfrac{27\sqrt{13}}{13}\left(cm\right)\\AH=\dfrac{18\sqrt{13}}{13}\left(cm\right)\end{matrix}\right.\)

a.
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm) theo định lý Pitago
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6$ (cm) theo định lý Pitago
$CH=BC-BH=10-3,6=6,4$ (cm)
b.
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH$
$\Rightarrow BH=\frac{AH^2}{CH}=\frac{AH^2}{CH}=\frac{9,6^2}{12,8}=7,2$ (cm)
$BC=BH+CH=7,2+12,8=20$ (cm)
$AB=\sqrt{AH^2+BH^2}=\sqrt{9,6^2+7,2^2}=12$ (cm) theo Pitago
$AC=\sqrt{BC^2-AB^2}=\sqrt{20^2-12^2}=16$ (cm) theo Pitago
c.
$AB.AC=AH.BC=12.25=300$
$AB^2+AC^2=BC^2=625$
$(AB+AC)^2-2AB.AC=625$
$AB+AC=\sqrt{625+2AB.AC}=\sqrt{625+2.300}=35$
Áp dụng Viet đảo thì $AB,AC$ là nghiệm của:
$X^2-35X+300=0$
$\Rightarrow (AB,AC)=(20,15)$ (giả sử $AB>AC$)
$BH=\sqrt{AB^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)

f) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB\cdot HC=12^2=144\)(1)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên BH+CH=25
hay BH=25-CH(2)
Thay (2) vào (1), ta được:
\(HC\left(25-HC\right)=144\)
\(\Leftrightarrow HC^2-25HC+144=0\)
\(\Leftrightarrow\left[{}\begin{matrix}HC=16\\HC=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}HB=9\\HB=16\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AB\in\left\{15;20\right\}\\AC\in\left\{20;15\right\}\end{matrix}\right.\)

Hướng dẫn:
∆
ABC ∼
∆
HBA nên 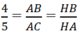
Suy ra HB = 4/5HA = 48/5 = 9,6. Chọn B.

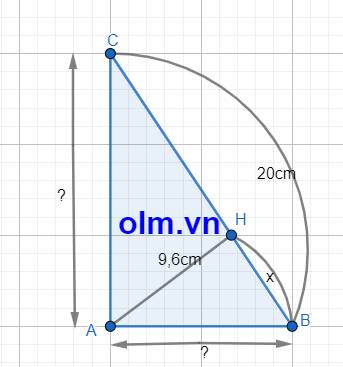
Gọi độ dài đoạn BH là: \(x\) ( cm) ; \(x\) > 0; AC > AB nên \(x\) < CH
Xét tam giác vuông HAB vuông tại H theo pytago ta có:
AB2 = HA2 + HB2 = 9,62 + \(x^2\) = 92,16 + \(x^2\)
Xét tam giác vuông AHC vuông tại H theo pytago ta có:
AC2 = HA2 + HC2 = 9,62 + (\(20-x\))2 = 92,16 + 400 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(x\) + \(x^2\)
Xét tam giác vuông ABC vuông tại A theo pytago ta có:
AC2 + AB2 = BC2
492,16 - 40\(x\) + \(x^2\) + 92,16 + \(x^2\) = 202
(\(x^2\) + \(x^2\)) - 40\(x\) + (492,16 + 92,16) - 400 = 0
2\(x^2\) - 40\(x\) + 584,32 - 400 = 0
2\(x^2\)- 40\(x\) + 184,32 =0
\(x^2\) - 20\(x\) + 92,16 = 0
△' = 102 - 92,16 = 7,84 > 0
\(x\)1 = -(-10) + \(\sqrt{7,84}\) = 12,8 ⇒ CH = 20 - 12,8 = 7,2 < BH (loại )
\(x_2\) = -(-10) - \(\sqrt{7,84}\) = 7,2 ⇒ CH = 20 - 7,2 = 12,8 (thỏa mãn)
Thay \(x_2\) = 7,2 vào biểu thức: AB2 = 92,16 + \(x^2\) = 92,16 + 7,22 = 144
⇒AB = \(\sqrt{144}\) = 12
Thay \(x_2\) = 7,2 vào biểu thức: AC2 = 492,16 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(\times\) 7,2 + 7,22 = 256
AC = \(\sqrt{256}\) = 16
Kết luận AB = 12 cm; AC = 16 cm

\(a,\)Áp dụng hệ thức lượng trong tam giác vuông ABC ta có
\(BC^2=AB^2+AC^2\Rightarrow BC^2=3^2+4^2\Rightarrow BC=\sqrt{9+16}\)
\(\Rightarrow BC=5cm\)
\(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}\Rightarrow BH=\frac{3^2}{5}=\frac{9}{5}cm\)
\(AC^2=CH.BC\Rightarrow CH=\frac{AC^2}{BC}\Rightarrow CH=\frac{4^2}{5}=\frac{16}{5}cm\)
\(AH^2=\frac{9}{5}.\frac{16}{5}\Rightarrow AH^2=\frac{144}{25}\Rightarrow AH=\sqrt{\frac{144}{25}}=\frac{12}{5}cm\)
\(b,\)
\(BC=BH+CH\Rightarrow BC=9+16\Rightarrow BC=25cm\)
\(AB^2=BH.BC\Rightarrow AB^2=9.25\Rightarrow AB=\sqrt{225}=15cm\)
\(AC^2=CH.BC\Rightarrow AC^2=16.25\Rightarrow AC=\sqrt{400}=20cm\)
\(AH^2=BH.CH\Rightarrow AH^2=9.16\Rightarrow AH=\sqrt{144}=12cm\)

a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; AC = 4cm
b, AB = 65cm; AC = 156cm; BC = 169cm; BH = 25cm
c, AB = 5cm; BC = 13cm; BH = 25/13cm; CH = 144/13cm
a) Áp dụng định lí Pytago trong \(\Delta\) AHC vuông tại H ta có :
\(AH^2+HC^2=AC^2\)
\(\Rightarrow HC^2=AC^2-AH^2\)
\(\Rightarrow HC=\sqrt{AC^2-AH^2}=\sqrt{40^2-24^2}=32cm\)
b) Áp dụng định lí Pytago trong \(\Delta\) AHC vuông tại H ta có :
\(AH^2+HC^2=AC^2\)
\(\Rightarrow AC=\sqrt{AH^2+HC^2}=\sqrt{9,6^2+12,8^2}=16cm\)
c) \(BC=CH+BH=72+12,5=84,5\left(cm\right)\)
Ta có: \(\left\{{}\begin{matrix}AB^2=BH.BC=12,5.84,5=1056,25\\AC^2=CH.BC=72.84,5=6084\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{65}{2}\left(cm\right)\\AC=78\left(cm\right)\end{matrix}\right.\)
Ta có: \(AB.AC=AH.BC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{78.\dfrac{65}{2}}{84,5}=30\left(cm\right)\)