K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
3
E
1 tháng 9 2021
\(<=>2x^2-5x+3=0\)
<=>\(2x^2-2x-3x+3=0\)
\(<=>2x(x-1)-3(x-1)=0\)
\(<=>(2x-3)(x-1)=0\)
th1 \(2x-3=0<=>x=3/2\)
th2 \(X-1=0<=>x=1\)
pt có tập nghiệm S={3/2;1}
1 tháng 9 2021
\(2x^3+3x^2-8x+3=0\\ \Rightarrow\left(2x^3-2x^2\right)+\left(5x^2-5x\right)-\left(3x-3\right)=0\\ \Rightarrow2x^2\left(x-1\right)+5x\left(x-1\right)-3\left(x-1\right)=0\\ \Rightarrow\left(x-1\right)\left(2x^2+5x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-1=0\\2x^2+5x-3=0\end{matrix}\right.\)
\(x-1=0\\ \Rightarrow x=1\)
\(2x^2+5x-3=0\\ \Rightarrow\left(2x^2+6x\right)-\left(x+3\right)=0\\ \Rightarrow2x\left(x+3\right)-\left(x+3\right)=0\\ \Rightarrow\left(x+3\right)\left(2x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+3=0\\2x-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-3\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy \(x=\left\{-3;\dfrac{1}{2};1\right\}\)
11 tháng 11 2017
Áp dụng quy tắc Horner , ta có :
Vậy , phaeps chia được thương bằng : x + 1
5 tháng 11 2021
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
H
18 tháng 4 2023
\(\dfrac{2x-6}{x+1}\ge0\)
`<=> 2x-6 >= 0`
`<=> 2x >=6`
`<=> x>=3`
Vật bpt đã cho có tập nghiệm \(S=\left\{x|x\ge3\right\}\)
26 tháng 8 2021
Bài 60:
a: Xét ΔMNP có
B là trung điểm của NP
A là trung điểm của MN
Do đó: AB là đường trung bình của ΔMNP
Suy ra: AB//MP và \(AB=\dfrac{MP}{2}\)
hay MP=10cm
b: Xét tứ giác ABPM có AB//PM
nên ABPM là hình thang
mà \(\widehat{PMA}=90^0\)
nên ABPM là hình thang vuông
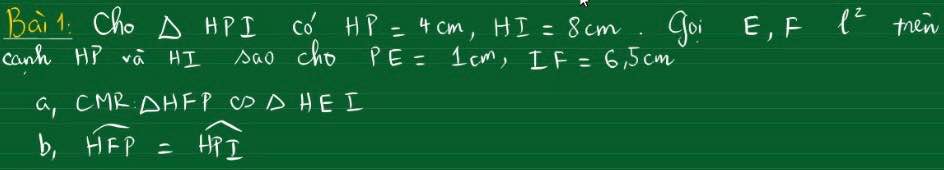
3:
a: Xét ΔACH vuông tại H và ΔBCA vuông tại A có
góc C chung
=>ΔACH đồng dạng vơi ΔBCA
b: Xét ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC