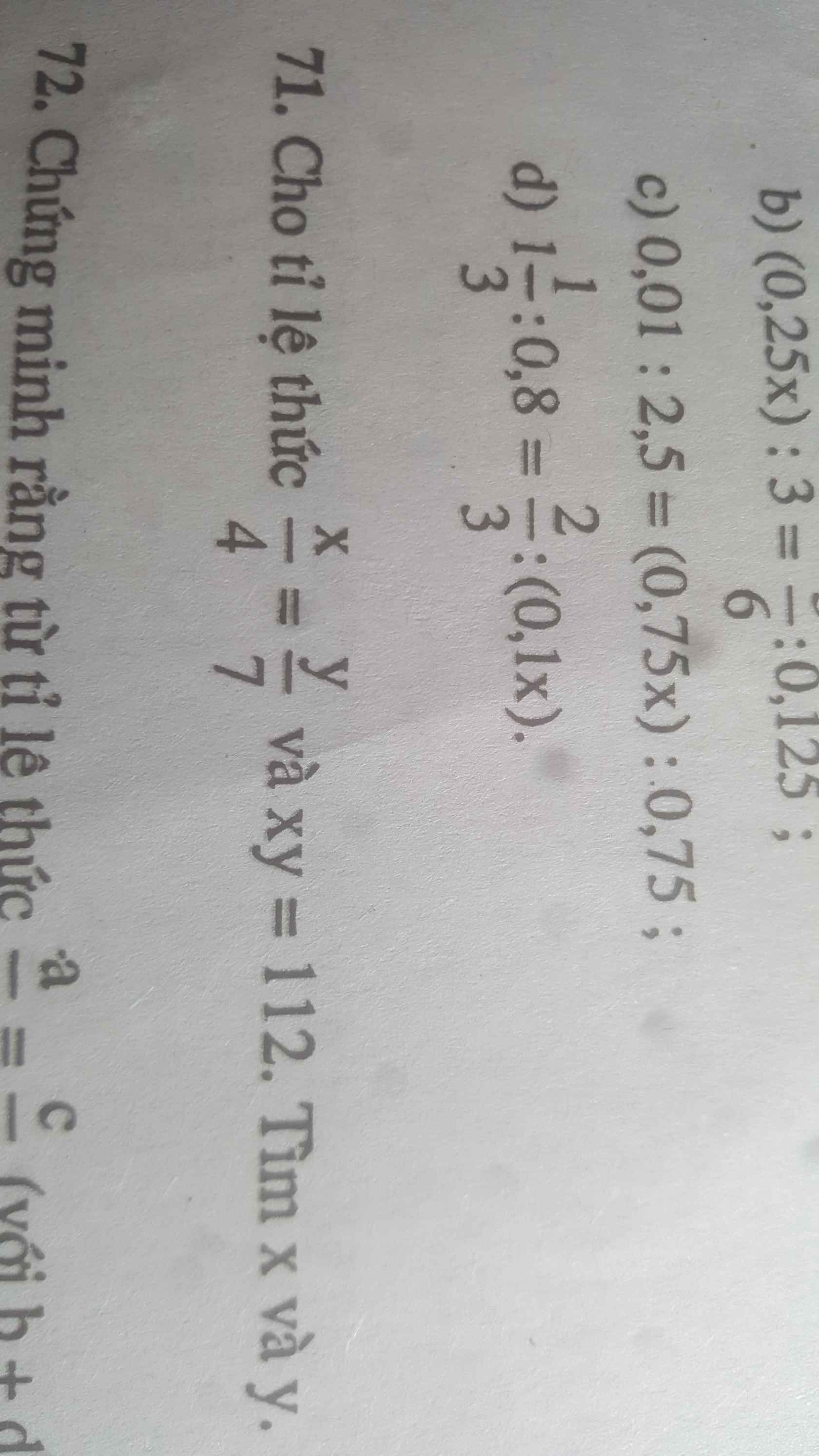K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Mọi người giúp em Câu 4 với ạ! Em cám ơn mn trc ạ!
8 tháng 1 2022
a: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AC//BE và AC=BE
b: Xét tứ giác AIEK có
AI//KE
AI=KE
Do đó: AIEK là hình bình hành
Suy ra: Hai đường chéo AE và IK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AE
nên M là trung điểm của IK
hay I.M,K thẳng hàng
30 tháng 6 2015
a) AE là phân giác => góc CAE=GÓC EAK=1/2 GÓC A=1/2 60=30
XÉT TAM GIÁC CAE VÀ TAM GIÁC KAE
GÓC C= GÓC K (=90)
AE CHUNG
GÓC CAE=GÓC EAK
=> 2 TAM GIÁC = NHAU ( CH.GN) => AK=AC
B) TAM GIÁC ABC: C=90 => GÓC A+B=90 => B=90-A=90-60=30
MÀ GÓC EAB=30 (CMT) => GÓC EAB=GÓC B => TAM GIÁC AEB CÂN TẠI E. EK LÀ ĐƯỜNG CAO => ĐỒNG THỜI LÀ TRUNG TUYẾN=> K LÀ TRUNG ĐIỂM AB => AK=1/2 AB. MÀ AK=AC => AC=1/2 AB
C) TAM GIÁC AEB CÂN => AE=EB
XÉT TAM GIÁC AEC VÀ TAM GIÁC BED:
C=D=90
AE=EB
2 GÓC TẠI D ĐỐI ĐỈNH
=> 2 TAM GIÁC BẰNG NHAU (CH.GN) => AC=BD
TAM GIÁC ABC VUÔNG TẠI C => THEO PY TA GO TA CÓ: \(BC^2=AB^2-AC^2\)
TAM GIÁC BED VUÔNG TẠI D. => \(AD^2=AB^2-BD^2\). MÀ BD=AC => BC=AD
26 tháng 9 2021
Đặt \(\dfrac{x}{4}=\dfrac{y}{7}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k\\y=7k\end{matrix}\right.\)
Ta có: xy=112
\(\Leftrightarrow28k^2=112\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=4\cdot2=8\\y=7k=7\cdot2=14\end{matrix}\right.\)
Trường hợp 2: x=-2
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=-8\\y=7k=-14\end{matrix}\right.\)
2 tháng 10 2021
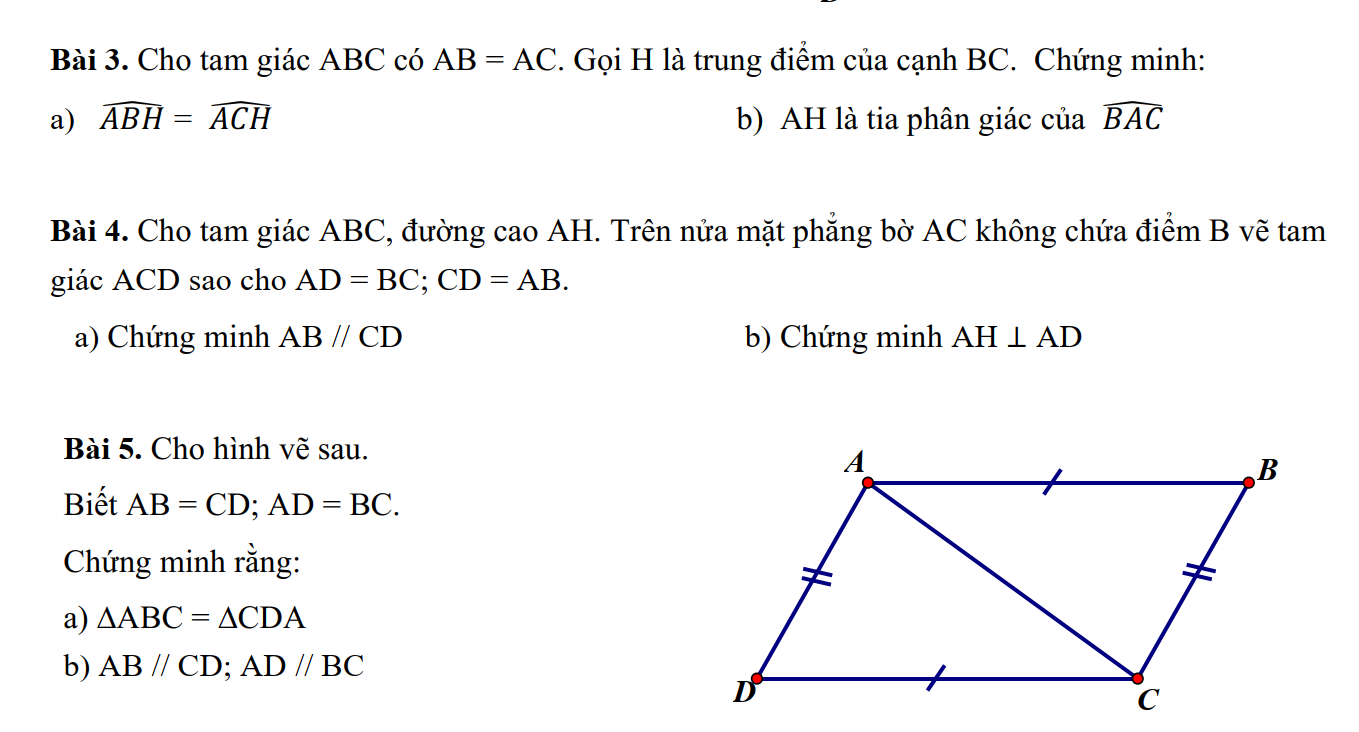
\(5,\\ a,\left\{{}\begin{matrix}AB=CD\left(gt\right)\\AD=BC\left(gt\right)\\AC.chung\end{matrix}\right.\Rightarrow\Delta ABC=\Delta CDA\left(c.c.c\right)\\ b,\Delta ABC=\Delta CDA\left(cm.trên\right)\\ \Rightarrow\left\{{}\begin{matrix}\widehat{CAB}=\widehat{DCA}\\\widehat{CAD}=\widehat{ACB}\end{matrix}\right.\left(các.cặp.góc.tương.ứng\right)\)
Mà các cặp góc này ở vị trí so le trong nên \(AB//CD;AD//BC\)
BK
1
VT
Vũ Thị Minh Ánh
Giáo viên
18 tháng 12 2022
\(A=\left|x-1\right|+\left|x+3\right|=\left|1-x\right|+\left|x+3\right|\)
\(A\ge\left|1-x+x+3\right|=4\)
Vậy giá trị nhỏ nhất của biểu thức A là 4.
NN
2
