Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình làm mẫu cho bạn câu a) nhé
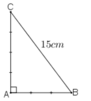
a) Theo định lí Pytago ta có :
BC2 = AB2 + AC2
152 = AB2 + AC2
AB : AC = 3:4
=> \(\frac{AB}{3}=\frac{AC}{4}\)=> \(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}\)và AB2 + AC2 = 152
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}=\frac{AB^2+AC^2}{3^2+4^2}=\frac{15^2}{25}=\frac{225}{25}=9\)
\(\frac{AB^2}{3^2}=9\Rightarrow AB^2=81\Rightarrow AB=\sqrt{81}=9cm\)
\(\frac{AC^2}{4^2}=9\Rightarrow AC^2=144\Rightarrow AC=\sqrt{144}=12cm\)
Ý b) tương tự nhé

b: Độ dài cạnh huyền là \(\sqrt{6^2+7^2}=\sqrt{85}\left(cm\right)\)
c: Số đo góc ở đỉnh là:
\(180-2\cdot20^0=140^0\)
d: Số đó góc ở đáy là:
\(\dfrac{180^0-60^0}{2}=60^0\)

Tam giác ABC vuông tại A => Áp dụng định lý pitago ta có : \(BC^2=AB^2+AC^2=26^2=676\) (cm)
\(\frac{AB}{AC}=\frac{5}{12}\Rightarrow\frac{AB}{5}=\frac{AC}{12}\Rightarrow\frac{AB^2}{25}=\frac{AC^2}{144}\) Áp dụng TCDTSBN ta có :
\(\frac{AB^2}{25}=\frac{AC^2}{144}=\frac{AB^2+AC^2}{25+144}=\frac{676}{169}=4=2^2\)
\(\Rightarrow\frac{AB}{5}=2\Rightarrow AB=10\left(cm\right)\)
\(\Rightarrow\frac{AC}{12}=2\Rightarrow AC=24\left(cm\right)\)
Vậy AB = 10 (cm); AC = 24 (cm)

Theo đề bài ta có:
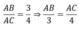
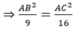
Theo tính chất dãy tỉ số bằng mhau ta có:
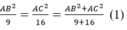
tam giác ABC vuông tại A
Áp dụng định lí pitago vào tam giác ABC ta có:
BC2 = AB2 + AC2 (2)
Từ (1) và (2) suy ra:
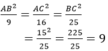
AB2 = 9. 9 = 81 ⇒ AB = 9 cm (vì AB > 0)
AC2 = 16. 9 = 144 ⇒ AC = 12 cm (vì AC > 0)

Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC

Bài 1:
Độ dài cạnh AB: ( 49 + 7 ) : 2 = 28 (cm)
Độ dài cạnh AC: 28 - 7 = 21 (cm)
Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A có:
\(BC^2=AC^2+AB^2\)
Hay \(BC^2=21^2+28^2\)
\(\Rightarrow BC^2=441+784\)
\(\Rightarrow BC^2=1225\)
\(\Rightarrow BC=35\left(cm\right)\)
Bài 2:
Áp dụng định lý Py-ta-go vào tam giác ABD vuông tại D có:
\(AB^2=AD^2+BD^2\)
\(\Rightarrow AD^2=AB^2-BD^2\)
Hay \(AD^2=17^2-15^2\)
\(\Rightarrow AD^2=289-225\)
\(\Rightarrow AD^2=64\)
\(\Rightarrow AD=8\left(cm\right)\)
Trong tam giác ABC có:
\(AD+DC=AC\)
\(\Rightarrow DC=AC-AD=17-8=9\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác BCD vuông tại D có:
\(BC^2=BD^2+DC^2\)
Hay \(BC^2=15^2+9^2\)
\(\Rightarrow BC^2=225+81\)
\(\Rightarrow BC^2=306\)
\(\Rightarrow BC=\sqrt{306}\approx17,5\left(cm\right)\)

a,Ta có : \(\dfrac{AB}{AC}=0,75\Rightarrow\dfrac{AB}{0,75}=AC\Rightarrow\dfrac{AB^2}{\dfrac{9}{16}}\:=AC^2\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{BA^2}{\dfrac{9}{16}}=AC^2=\dfrac{AB^2+AC^2}{\dfrac{9}{16}+1}=\dfrac{225}{\dfrac{25}{16}}=144\Rightarrow AB=9cm;AC=12cm\)
b, Ta có : \(S_{ABC}=\dfrac{1}{2}AB.AC;S_{ABC}=\dfrac{1}{2}AH.BC\Rightarrow AB.AC=AH.BC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{108}{15}cm\)
a,Ta có: \(\dfrac{AB}{AC}=0,75=\dfrac{3}{4}\Leftrightarrow\dfrac{AB^2}{AC^2}=\dfrac{9}{16}\)
\(\Rightarrow\dfrac{AB^2}{9}=\dfrac{AC^2}{16}=\dfrac{AB^2+AC^2}{9+16}=\dfrac{BC^2}{25}=\dfrac{15^2}{25}=9\)
\(\Rightarrow AB^2=9.9=81\Leftrightarrow AB=9\left(cm\right);AC^2=9.16=144\Leftrightarrow AC=12\left(cm\right)\)
b, Ta có: \(S_{ABC}=\dfrac{1}{2}.AB.AC\)
Mà \(S_{ABC}=\dfrac{1}{2}.AH.BC\)
\(\Rightarrow AB.AC=AH.BC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{9.12}{15}=7,2\left(cm\right)\)
a,
Áp dụng định lí Py-ta-go, ta có:
AB2 + AC2 = BC2
=> AB2 + AC2 = 225
Lại có:
AB:AC = 3:4
\(\Rightarrow\dfrac{AB^2}{AC^2}=\dfrac{9}{16}\)
Đặt tỉ số trên bằng k
=> AB2 = 9k và AC2 = 16k
=> AB2 + AC2 = 9k + 16k = 25k = 225
=> k = 9
\(\Rightarrow\left\{{}\begin{matrix}AB^2=9\cdot9=81\\AC^2=9\cdot16=144\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=9cm\\AC=12cm\end{matrix}\right.\)
b,
Áp dụng định lí Py-ta-go, ta có:
AB2 + AC2 = BC2
=> 576 + AC2 = BC2
Lại có:
AC:BC = 5:13
\(\Rightarrow\dfrac{AC^2}{BC^2}=\dfrac{25}{169}\)
Đặt tỉ số trên bằng k
=> AC2 = 25k và BC2 = 169k
=> 576 + 25k = 169k
=> 576 = 144k
=> k = 4
=> \(\left\{{}\begin{matrix}AC^2=4\cdot25=100\\BC^2=4\cdot169=676\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AC=10cm\\BC=26cm\end{matrix}\right.\)