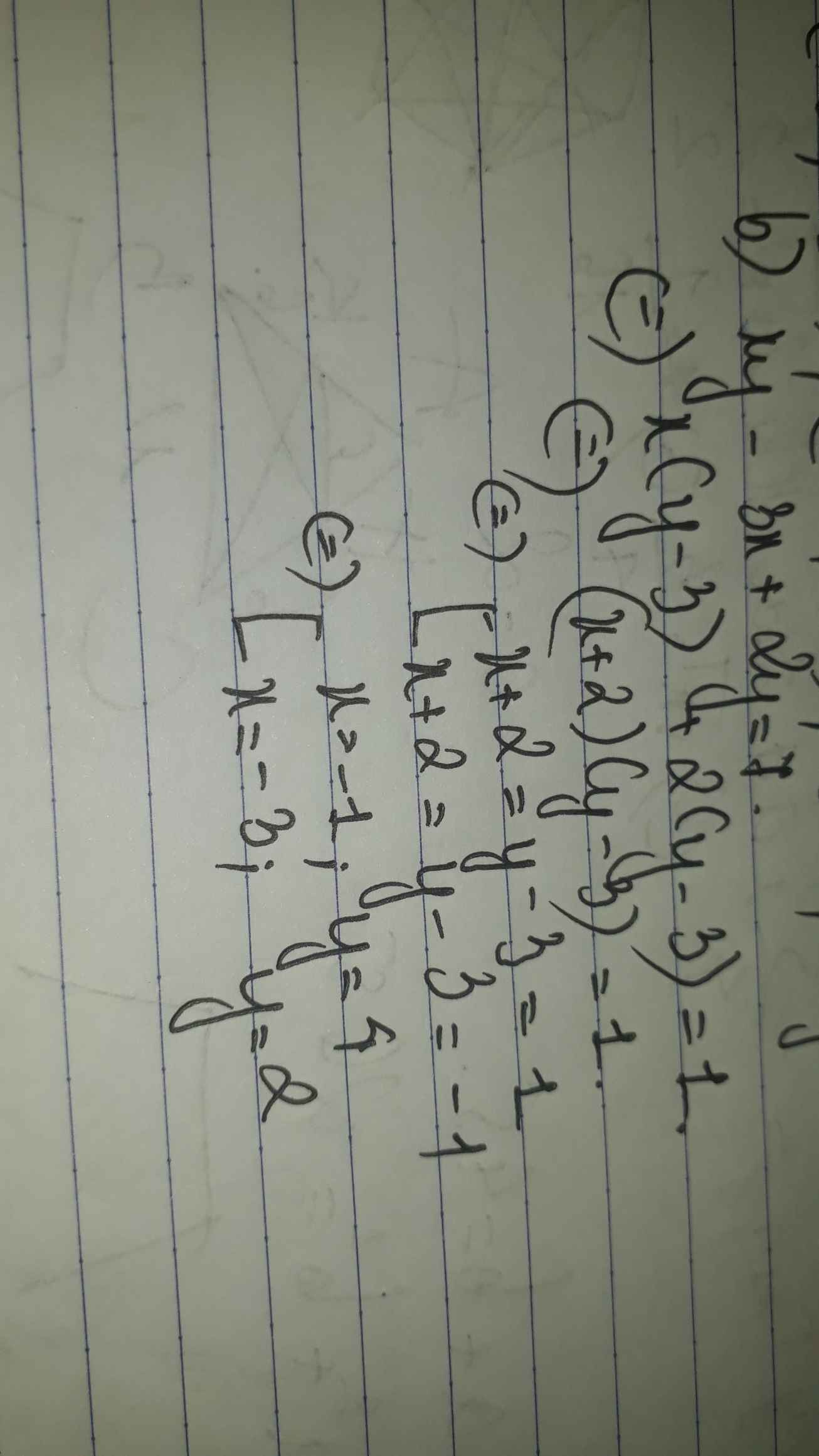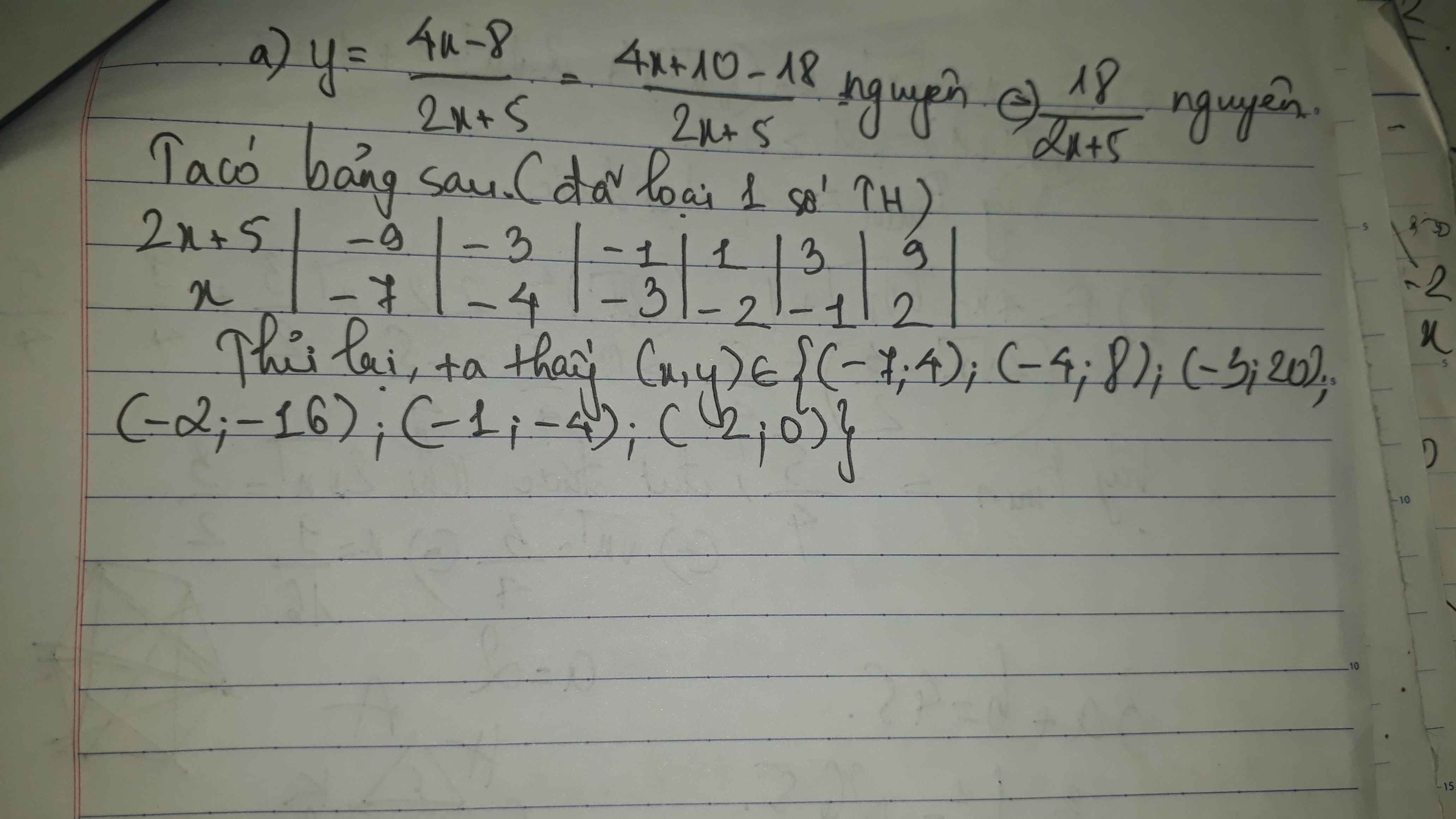LH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LH
1
17 tháng 7 2021
a) Để y nguyên thì \(6x-4⋮2x+3\)
\(\Leftrightarrow-13⋮2x+3\)
\(\Leftrightarrow2x+3\in\left\{1;-1;13;-13\right\}\)
\(\Leftrightarrow2x\in\left\{-2;-4;10;-16\right\}\)
hay \(x\in\left\{-1;-2;5;-8\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
\(y=\dfrac{2\left(2x+5\right)-18}{2x+5}=2-\dfrac{18}{2x+5}\)
\(y\in Z\Rightarrow\dfrac{18}{2x+5}\in Z\Rightarrow2x+5=Ư\left(18\right)\)
Mà 2x+5 luôn lẻ nên ta có: \(2x+5=\left\{-9;-3;-1;1;3;9\right\}\)
| 2x+5 | -9 | -3 | -1 | 1 | 3 | 9 |
| x | -7 | -4 | -3 | -2 | -1 | 2 |
| y | 4 | 8 | 20 | -16 | -4 | 0 |
LH
2
A
21 tháng 7 2021
c, x/2+1/y=1/3 (x,y∈Z)
⇒1/y=1/3-x/2
⇒1/y=2-3x/6
⇒y(2-3x)=6
⇒y∈Ư(6)∈{1;-1;2;-2;3;-3;6;-6}
| y | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| 2-3x | 6 | -6 | 3 | -3 | 2 | -2 | 1 | -1 |
| 3x | -4 | 8 | -1 | 5 | 0 | 4 | 1 | 3 |
| x | -4/3 (loại) | 8/3(loại) | -1/3(loại) | 5/3(loại) | 0 | 4/3(loại) | 1/3(loại) | 1
|
Vậy các cặp (x;y) thỏa mãn pt trên là (0;3);(1;-6)
4 tháng 7 2017
2.
a) \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{2x+3y+5z}{6+12+25}=\frac{86}{43}=2\)
\(\Rightarrow x=6;y=8;z=10\)
b) \(\frac{x}{3}=\frac{y}{4}\Rightarrow\frac{x}{18}=\frac{y}{24}\)( 1 )
\(\frac{y}{6}=\frac{z}{8}\Rightarrow\frac{y}{24}=\frac{z}{32}\)( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\frac{x}{18}=\frac{y}{24}=\frac{z}{32}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{x}{18}=\frac{y}{24}=\frac{z}{32}=\frac{3x-2y-z}{54-48-32}=\frac{13}{-26}=\frac{-1}{2}\)
\(\Rightarrow x=-9;y=-12;z=-16\)
3.
a) \(\frac{x}{3}=\frac{y}{7}=\frac{z}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{x}{3}=\frac{y}{7}=\frac{z}{2}=\frac{2x^2+y^2+3z^2}{18+49+12}=\frac{316}{79}=4\)
\(\Rightarrow x=12;y=28;z=8\)
b) x : y : z = 2 : 5 : 7
\(\Rightarrow\frac{x}{2}=\frac{y}{5}=\frac{z}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{x}{2}=\frac{y}{5}=\frac{z}{7}=\frac{3x+2y-z}{6+10-7}=\frac{27}{9}=3\)'
\(\Rightarrow x=6;y=15;z=21\)
K
4 tháng 7 2017
2) a, \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\Rightarrow\frac{2x}{6}=\frac{3y}{12}=\frac{5z}{25}=\frac{2x+3y+5z}{6+12+25}=\frac{86}{43}=2\) (theo t/c dãy tỉ số bằng nhau)
=> x = 2.3 = 6 ; y = 2.4 = 8; z = 2.5 = 10
b, \(\frac{x}{3}=\frac{y}{4}\Rightarrow\frac{x}{9}=\frac{y}{12}\)
\(\frac{y}{6}=\frac{z}{8}\Rightarrow\frac{y}{12}=\frac{z}{16}\)
\(\Rightarrow\frac{x}{9}=\frac{y}{12}=\frac{z}{16}\Rightarrow\frac{3x}{27}=\frac{2y}{24}=\frac{z}{16}=\frac{3x-2y-z}{27-24-16}=\frac{13}{-13}=-1\) (theo t/c của dãy tỉ số bằng nhau)
=> x=(-1).9=-9 ; y=(-1).12=-12 ; z=(-1).16=-16
c, Đặt \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=k\Rightarrow x=2k;y=3k;z=4k\)
Ta có: xy+yz+zx=104
=> (2k)(3k) + (3k)(4k) + (4k)(2k) = 104
=> 6k2 + 12k2 + 8k2 = 104
=> k2(6+12+8) = 104
=> 26k2 = 104
=> k2 = 4
=> k = ±2
Với k = 2 thì \(\hept{\begin{cases}x=2.2=4\\y=2.3=6\\z=2.4=8\end{cases}}\)
Với k = -2 thì \(\hept{\begin{cases}x=2.\left(-2\right)=-4\\y=\left(-2\right).3=-6\\z=\left(-2\right).4=-8\end{cases}}\)
3) a, Đặt k=x/3=y/7=z/2
\(k=\frac{x}{3}=\frac{y}{7}=\frac{z}{2}\Rightarrow k^2=\frac{x^2}{9}=\frac{y^2}{49}=\frac{z^2}{4}=\frac{2x^2}{18}=\frac{y^2}{49}=\frac{3z^2}{12}=\frac{2x^2+y^2+3z^2}{18+49+12}=\frac{316}{79}=4\)
=> k2 = 4 => k = ±2
Với k = 2 thì \(\hept{\begin{cases}\frac{x}{2}=2\Rightarrow x=4\\\frac{y}{3}=2\Rightarrow y=6\\\frac{z}{4}=2\Rightarrow z=8\end{cases}}\)
Với k = -2 thì \(\hept{\begin{cases}\frac{x}{2}=-2\Rightarrow x=-4\\\frac{y}{3}=-2\Rightarrow y=-6\\\frac{z}{4}=-2\Rightarrow z=-8\end{cases}}\)
b, \(x:y:z=2:5:7\Rightarrow\frac{x}{2}=\frac{y}{5}=\frac{z}{7}\Rightarrow\frac{3x}{6}=\frac{2y}{10}=\frac{z}{7}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{3x}{6}=\frac{2y}{10}=\frac{z}{7}=\frac{3x+2y-z}{6+10-7}=\frac{27}{9}=3\)
=> x = 2.3 = 6 ; y = 5.3 = 15 ; z = 7.3 = 21
AH
Akai Haruma
Giáo viên
29 tháng 12 2022
Lời giải:
$\frac{x}{y}=\frac{2}{3}\Rightarrow \frac{x}{2}=\frac{y}{3}$. Đặt $\frac{x}{2}=\frac{y}{3}=k$ thì:
$x=2k; y=3k$
Khi đó: $3x-2y=3.2k-3.2k=0$. Mẫu số không thể bằng $0$ nên $A$ không xác định. Bạn xem lại.
$B=\frac{2(2k)^2-2k.3k+3(3k)^2}{3(2k)^2+2.2k.3k+(3k)^2}=\frac{29k^2}{33k^2}=\frac{29}{33}$
TV
1
26 tháng 12 2021
\(\dfrac{3x-2y}{4}=\dfrac{4y-3z}{2}=\dfrac{2z-4x}{3}=\dfrac{12x-8y}{16}=\dfrac{6z-12x}{9}=\dfrac{8y-6z}{4}=\dfrac{12x-8y+6z-12x+8y-6z}{16+9+4}=\dfrac{0}{29}=0\\ \Leftrightarrow\left\{{}\begin{matrix}3x-2y=0\\2z-4x=0\\4y-3z=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\\\dfrac{y}{3}=\dfrac{z}{4}\\\dfrac{z}{4}=\dfrac{x}{2}\end{matrix}\right.\\ \Leftrightarrow\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x-2y+3z}{2-6+12}=\dfrac{8}{8}=1\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\\z=4\end{matrix}\right.\)
