K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ML
30 tháng 6 2017
a) 12 . ( x - 1 ) = 0
x - 1 = 0 : 12
x - 1 = 0
x = 0 + 1
x = 1
b) ( 6x - 39 ) : 3 = 201
6x - 39 = 201 . 3
6x - 39 = 603
6x = 603 + 39
6x = 642
x = 642 : 6
x = 107
c) 23 + 3x = 56 : 53
23 + 3x = 53
23 + 3x = 125
3x = 125 - 23
3x = 102
x = 102 : 3
x = 34
Các phần d , e , f Đỗ Ngọc Hoàng Hải làm tương tự như phần trên .
30 tháng 6 2017
a/x =1 nha
b/(6x-39):3=201
6x-39 =201x3
6x-39 =603
6x = 603+39
6x = 642
6= 642:6=107
c/ 23+3.x=125
3x= 125-23=102
x= 102:3=34
d/ 541+(281-x)=735
281-x= 735-541=194
x=281-194=87
e/ 9x+2=20
9x=20-2
9x=18
x=18:9=9
f/71+(26-3x):5=75
(26-3x):5=75-71=4
26-3x=4x5=20
3x=26-20=6
x=6:3=2
tk nha ^^
29 tháng 8 2021
17: \(x-\sqrt{x}-2=\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
18: \(x-3\sqrt{x}+2=\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)\)
19: \(x\sqrt{x}-x+\sqrt{x}-1=\left(\sqrt{x}-1\right)\left(x+1\right)\)
20: \(x\sqrt{x}+y\sqrt{y}+x-y\)
\(=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)+\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)\)
\(=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y+\sqrt{x}-\sqrt{y}\right)\)
HV
29 tháng 8 2021
\(17,=\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\\ 18,=\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)\\ 19,=\left(x+1\right)\left(\sqrt{x}-1\right)\\ 20,=???\)
bn xem lại đề câu 20 nha
tik mik nha
7 tháng 7 2021
1) Ta có: P=4
nên \(x-2\sqrt{x}+22=4\sqrt{x}+12\)
\(\Leftrightarrow x-6\sqrt{x}+10=0\)(Vô lý)
3) Thay \(x=3-2\sqrt{2}\) vào P, ta được:
\(P=\dfrac{3-2\sqrt{2}-2\left(\sqrt{2}-1\right)+22}{\sqrt{2}-1+3}\)
\(=\dfrac{3-2\sqrt{2}-2\sqrt{2}+2+22}{2+\sqrt{2}}\)
\(=\dfrac{27-4\sqrt{2}}{2+\sqrt{2}}\)
\(=\dfrac{\left(27-4\sqrt{2}\right)\left(\sqrt{2}-1\right)}{\sqrt{2}}\)
\(=\dfrac{\left(27\sqrt{2}-8\right)\left(\sqrt{2}-1\right)}{2}\)
\(=\dfrac{54-27\sqrt{2}-8\sqrt{2}+8}{2}\)
\(=\dfrac{64-35\sqrt{2}}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 8 2021
1.
ĐKXĐ: \(x< 5\)
\(\Leftrightarrow\sqrt{\dfrac{42}{5-x}}-3+\sqrt{\dfrac{60}{7-x}}-3=0\)
\(\Leftrightarrow\dfrac{\dfrac{42}{5-x}-9}{\sqrt{\dfrac{42}{5-x}}+3}+\dfrac{\dfrac{60}{7-x}-9}{\sqrt{\dfrac{60}{7-x}}+3}=0\)
\(\Leftrightarrow\dfrac{9x-3}{\left(5-x\right)\left(\sqrt{\dfrac{42}{5-x}}+3\right)}+\dfrac{9x-3}{\left(7-x\right)\left(\sqrt{\dfrac{60}{7-x}}+3\right)}=0\)
\(\Leftrightarrow\left(9x-3\right)\left(\dfrac{1}{\left(5-x\right)\left(\sqrt{\dfrac{42}{5-x}}+3\right)}+\dfrac{1}{\left(7-x\right)\left(\sqrt{\dfrac{60}{7-x}}+3\right)}\right)=0\)
\(\Leftrightarrow x=\dfrac{1}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 8 2021
b.
ĐKXĐ: \(x\ge2\)
\(\sqrt{\left(x-2\right)\left(x-1\right)}+\sqrt{x+3}=\sqrt{x-2}+\sqrt{\left(x-1\right)\left(x+3\right)}\)
\(\Leftrightarrow\sqrt{\left(x-2\right)\left(x-1\right)}-\sqrt{x-2}+\sqrt{x+3}-\sqrt{\left(x-1\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\sqrt{x-2}\left(\sqrt{x-1}-1\right)-\sqrt{x+3}\left(\sqrt{x-1}-1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)\left(\sqrt{x-2}-\sqrt{x+3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}-1=0\\\sqrt{x-2}-\sqrt{x+3}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=1\\x-2=x+3\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=2\)
CM
28 tháng 11 2017
a)
( x − 3 ) 2 + ( x + 4 ) 2 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 + 3 x − 23 = 0 ⇔ 2 x 2 + 5 x + 2 = 0
Có a = 2; b = 5; c = 2 ⇒ Δ = 5 2 – 4 . 2 . 2 = 9 > 0
⇒ Phương trình có hai nghiệm:
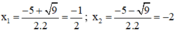
Vậy phương trình có tập nghiệm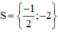 
b)
x 3 + 2 x 2 − ( x − 3 ) 2 = ( x − 1 ) x 2 − 2 ⇔ x 3 + 2 x 2 − x 2 − 6 x + 9 = x 3 − x 2 − 2 x + 2 ⇔ x 3 + 2 x 2 − x 2 + 6 x − 9 − x 3 + x 2 + 2 x − 2 = 0 ⇔ 2 x 2 + 8 x − 11 = 0
Có a = 2; b = 8; c = -11 ⇒ Δ ’ = 4 2 – 2 . ( - 11 ) = 38 > 0
⇒ Phương trình có hai nghiệm:
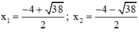
Vậy phương trình có tập nghiệm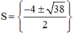 
c)
( x − 1 ) 3 + 0 , 5 x 2 = x x 2 + 1 , 5 ⇔ x 3 − 3 x 2 + 3 x − 1 + 0 , 5 x 2 = x 3 + 1 , 5 x ⇔ x 3 + 1 , 5 x − x 3 + 3 x 2 − 3 x + 1 − 0 , 5 x 2 = 0 ⇔ 2 , 5 x 2 − 1 , 5 x + 1 = 0
Có a = 2,5; b = -1,5; c = 1
⇒ Δ = ( - 1 , 5 ) 2 – 4 . 2 , 5 . 1 = - 7 , 75 < 0
Vậy phương trình vô nghiệm.
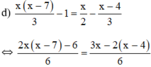
⇔ 2 x ( x − 7 ) − 6 = 3 x − 2 ( x − 4 ) ⇔ 2 x 2 − 14 x − 6 = 3 x − 2 x + 8 ⇔ 2 x 2 − 14 x − 6 − 3 x + 2 x − 8 = 0 ⇔ 2 x 2 − 15 x − 14 = 0
Có a = 2; b = -15; c = -14
⇒ Δ = ( - 15 ) 2 – 4 . 2 . ( - 14 ) = 337 > 0
⇒ Phương trình có hai nghiệm:
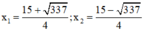
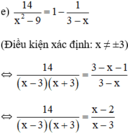
⇔ 14 = ( x - 2 ) ( x + 3 ) ⇔ 14 = x 2 - 2 x + 3 x - 6 ⇔ x 2 + x - 20 = 0
Có a = 1; b = 1; c = -20
⇒ Δ = 1 2 – 4 . 1 . ( - 20 ) = 81 > 0
Phương trình có hai nghiệm:
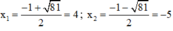
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có tập nghiệm S = {-5; 4}.
f) Điều kiện: x≠-1;x≠4
Ta có: a= 1, b = -7, c = - 8
∆ = ( - 7 ) 2 – 4 . 1 . ( - 8 ) = 81
=> Phương trình có hai nghiệm:
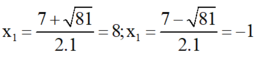
Kết hợp với diều kiện, nghiệm của phương trình đã cho là x = 8
6 tháng 4 2023
1: =>x^2+3x-4=0
=>(x+4)(x-1)=0
=>x=1 hoặc x=-4
2: =>2x-3y=1 và 3x=4y+2
=>2x-3y=1 và 3x-4y=2
=>x=2 và y=1
541 + ( 218 - x ) = 735
=> 541 + 218 - x = 735
=> x = 541 + 218 - 735
=> x = 24
96 - 3 . ( x + 1 ) = 42
=> 3 . ( x + 1 ) = 96 - 42
=> 3 . ( x + 1 ) = 54
=> x + 1 = 54 : 3
=> x + 1 = 18
=> x = 18 - 1
=> x = 17
541+(218-x)=735
218-x = 735-541
218-x = 194
x=218-194=24
96-3.(x+1)=42
3.(x+1)=96-42
3.(x+1)=54
x+1=54:3=18
x=18-1=17