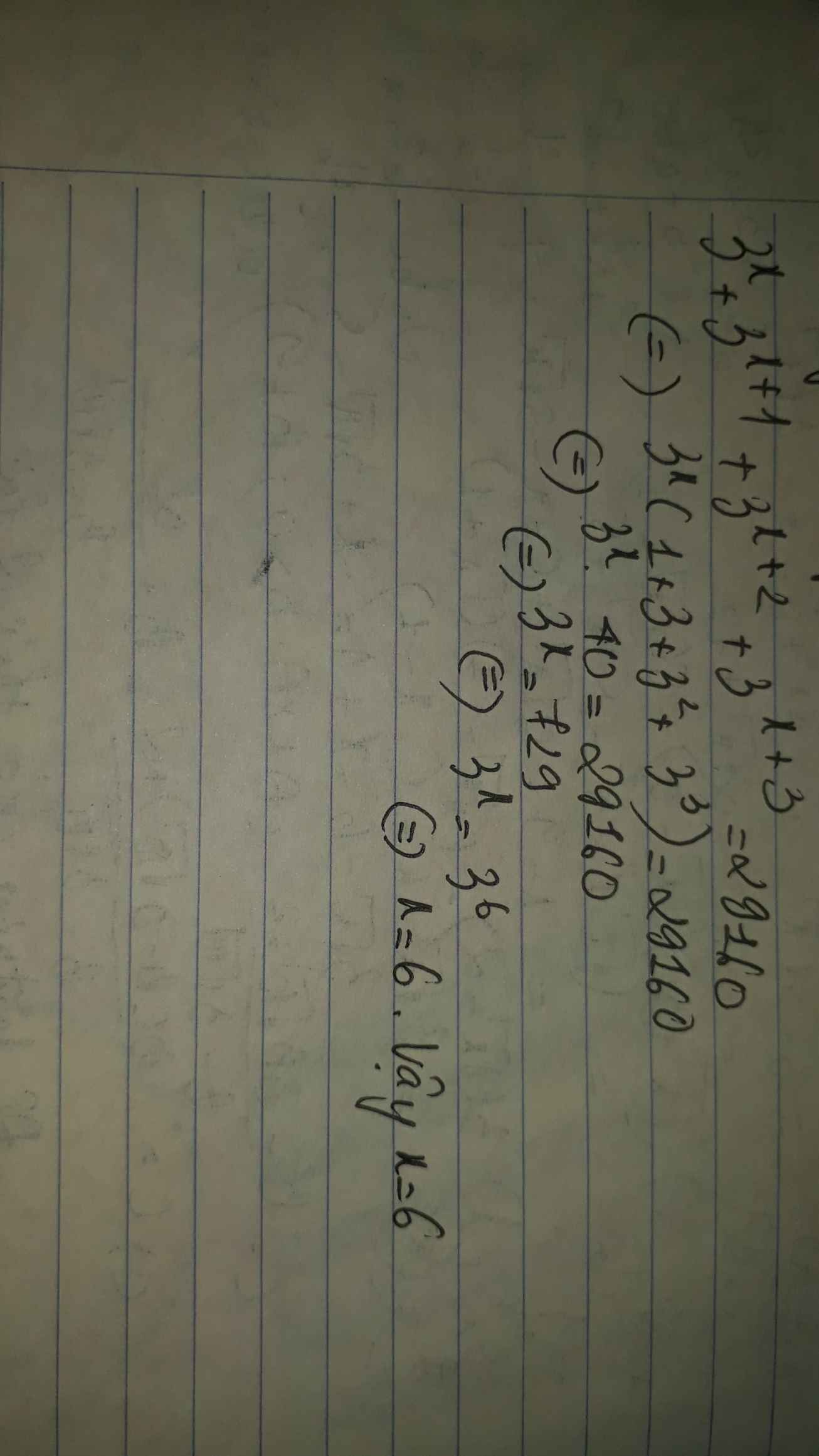K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2023
Em kiểm tra lại đề bài, \(3^x+3^{x+2}+3^{x+2}\) hay \(3^x+3^{x+1}+3^{x+2}\)
19 tháng 1 2022
$\Rightarrow 3^x(1+3+3^2+3^3)=1080$
$\Rightarrow 3^x.40=1080$
$\Rightarrow 3^x=27=3^3$
$\Rightarrow x=3$
N
1
NM
20 tháng 11 2019
a,(2x-1)3 =23+102 b,(3x+1)+(3x+3)+...+(3x+99)=2800
(2x-1)3 =125 3x+1+3x+3+...+3x+99=2800
(2x-1)3=53 ( 3x+3x+.....+3x )+(1+3+...+99)=2800
2x-1=5 gọi A=3x+3x+...+3x ; B=1+3+...+99
2x=5+1 số số hạng của B là : (99-1):2+1=50 ( bằng số số hạng của A)
2x=6 B = (99+1) x 50:2
=2500
x=6:2 ta có: 150x + 2500=2800
x=3 150x=2800-2500
vậy x=3 150x=300
x=300:150
x=2
vậy x=2
25 tháng 8 2021
Ta có: \(3x+3x+1+3x+2+3x+3=29160\)
\(\Leftrightarrow12x=29154\)
hay x=2429,5
25 tháng 8 2021
\(3x+3x+1+3x+2+3x+3=29160\Rightarrow3x+3x+3x+3x=29160-1-2-3\)
\(\Rightarrow12x=29154\Rightarrow x=\dfrac{4859}{2}=2429,5\)
9 tháng 9 2021
Ta có: \(3^x+3^{x+2}+3^{x+3}=3^5\cdot37\)
\(\Leftrightarrow3^x\cdot\left(1+9+27\right)=3^5\cdot37\)
hay x=5
