K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2023
Em kiểm tra lại đề bài, \(3^x+3^{x+2}+3^{x+2}\) hay \(3^x+3^{x+1}+3^{x+2}\)
19 tháng 1 2022
$\Rightarrow 3^x(1+3+3^2+3^3)=1080$
$\Rightarrow 3^x.40=1080$
$\Rightarrow 3^x=27=3^3$
$\Rightarrow x=3$
25 tháng 8 2021
Ta có: \(3x+3x+1+3x+2+3x+3=29160\)
\(\Leftrightarrow12x=29154\)
hay x=2429,5
25 tháng 8 2021
\(3x+3x+1+3x+2+3x+3=29160\Rightarrow3x+3x+3x+3x=29160-1-2-3\)
\(\Rightarrow12x=29154\Rightarrow x=\dfrac{4859}{2}=2429,5\)
PK
0
LQ
3
8 tháng 10 2021
\(\left(3x-1\right)^3=25\left(3x-1\right)\\ \Leftrightarrow\left(3x-1\right)^2=25\\ \Leftrightarrow\left[{}\begin{matrix}3x-1=5\\3x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\\ \left(3x-14\right)^3=2^5\cdot5^2+200\\ \Leftrightarrow\left(3x-14\right)^3=1000=10^3\\ \Leftrightarrow3x-14=10\Leftrightarrow x=8\)
8 tháng 10 2021
\(\left(3x-1\right)^3=25\left(3x-1\right)\)
\(\Rightarrow\left(3x-1\right)\left(9x^2-6x+1-25\right)=0\)
\(\Rightarrow\left(3x-1\right)\left(9x^2-6x-24\right)=0\)
\(\Rightarrow3\left(3x-1\right)\left(x-2\right)\left(3x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\)
\(\left(3x-14\right)^3=2^5.5^2+200\)
\(\Rightarrow\left(3x-14\right)^3=1000\)
\(\Rightarrow3x-14=10\Rightarrow3x=24\Rightarrow x=8\)
NN
1
26 tháng 5 2017
1, 4[3x + 4] = 12x + 16
2, 4/3[5/3x + 6] = 20/9x + 12
3, [4/3x + 7]. 5 + 2 = 20/3x + 35 + 2 = 20/3x + 37
4, [3/7x - 6][-7] + 3x = -3x + 42 + 3x = 42
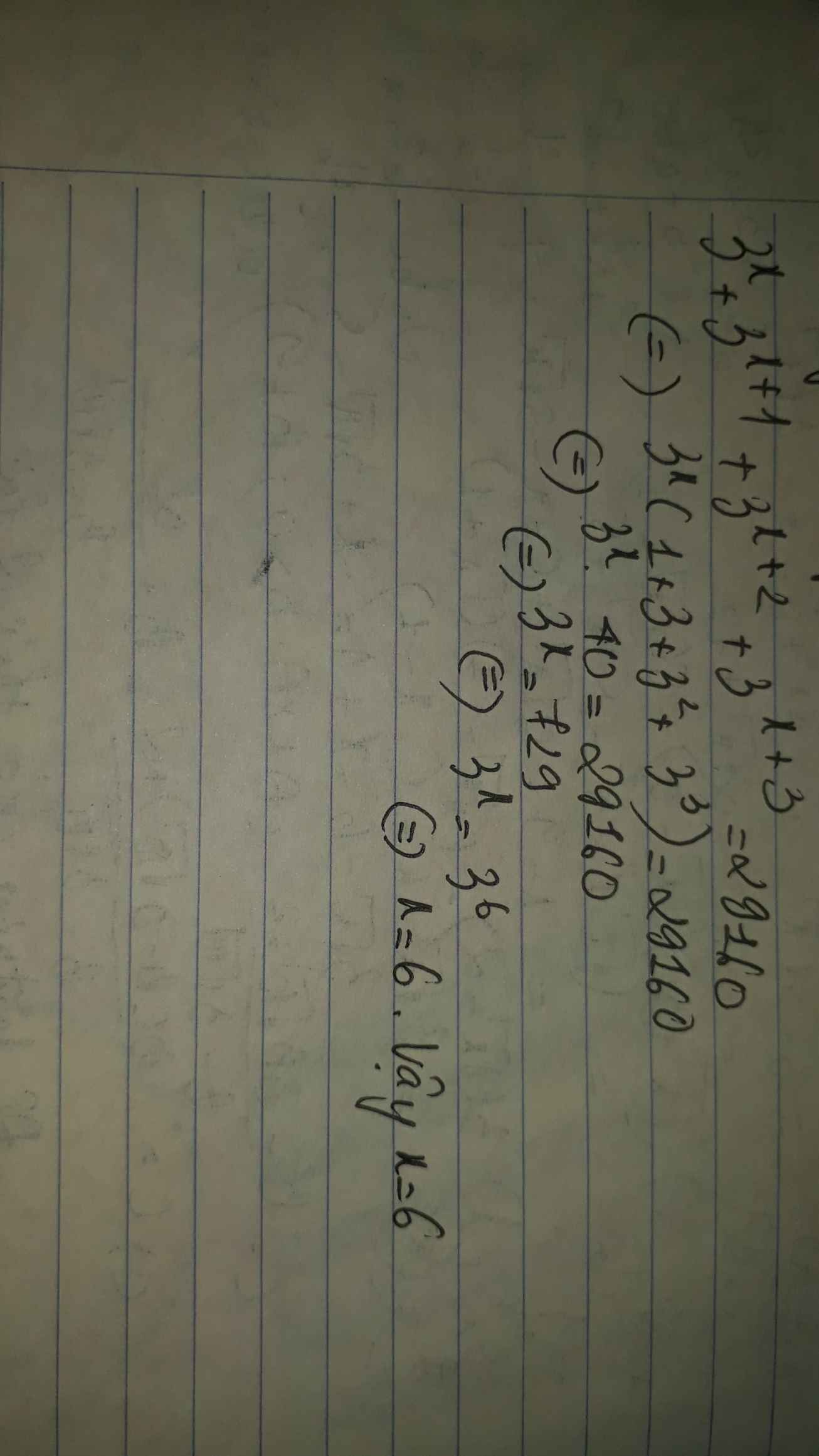
Ta có: \(3^x+3^{x+2}+3^{x+3}=3^5\cdot37\)
\(\Leftrightarrow3^x\cdot\left(1+9+27\right)=3^5\cdot37\)
hay x=5