
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Sửa đề: \(\dfrac{1}{1.9}\rightarrow\dfrac{9}{9.19}\)
Giải:
\(N=\dfrac{9}{9.19}+\dfrac{9}{19.29}+\dfrac{9}{29.39}+...+\dfrac{9}{2019.2029}\)
\(N=\dfrac{9}{10}.\left(\dfrac{10}{9.19}+\dfrac{10}{19.29}+\dfrac{10}{29.39}+...+\dfrac{10}{2019.2029}\right)\)
\(N=\dfrac{9}{10}.\left(\dfrac{1}{9}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{29}+\dfrac{1}{29}-\dfrac{1}{39}+...+\dfrac{1}{2019}-\dfrac{1}{2029}\right)\)
\(N=\dfrac{9}{10}.\left(\dfrac{1}{9}-\dfrac{1}{2029}\right)\)
\(N=\dfrac{9}{10}.\dfrac{2020}{18261}\)
\(N=\dfrac{202}{2029}\)

a: Xét ΔAHE vuông tại E và ΔAHI vuông tại I có
AH chung
góc EAH=góc IAH
=>ΔAHE=ΔAHI
b: HE=HI
=>HN=HM
Xét ΔAHN và ΔAHM có
AH chung
góc NHA=góc MHA
HN=HM
=>ΔAHN=ΔAHM
=>AN=AM
=>AH là trung trực của MN
=>AH vuông góc MN

Em nhân hệ số với hệ số, biến nhân biến (cùng chữ á)
(xo)2 thì đưa về bằng 12
Em tự làm thử nhé, anh sẽ sửa!

a) Để f(x) có bậc là 1 thì m=0
b) Thay x=-1 vào f(x), ta được:
\(m\cdot\left(-1\right)^2+3\cdot\left(-1\right)+6=0\)
\(\Leftrightarrow m+3=0\)
hay m=-3

a, \(|x-1|+|2x-y+3|=0\)
Ta có : \(|x-1|\ge0;|2x-y+3|\ge0< =>|x-1|+|2x-y+3|\ge0\)
Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x-1=0\\2x-y+3=0\end{cases}< =>\hept{\begin{cases}x=1\\y=5\end{cases}}}\)
b, \(|x-y|+|x+y-2|=0\)
Ta có : \(|x-y|\ge0;|x+y-2|\ge0< =>|x-y|+|x+y-2|\ge0\)
Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x-y=0\\x+y-2=0\end{cases}< =>\hept{\begin{cases}x=1\\y=1\end{cases}< =>x=y=1}}\)
c, \(|x+y-1|+|2x-3y|=0\)
Ta có : \(|x+y-1|\ge0;|2x-3y|\ge0< =>|x+y-1|+|2x-3y|\ge0\)
Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x+y-1=0\\2x-3y=0\end{cases}}< =>\hept{\begin{cases}x+y=1\\\frac{x}{3}=\frac{y}{2}\end{cases}}\)
Theo tính chất của dãy tỉ số bằng nhau ta có : \(\frac{x}{3}=\frac{y}{2}=\frac{x+y}{3+2}=\frac{1}{5}< =>\hept{\begin{cases}\frac{x}{3}=\frac{1}{5}\\\frac{y}{2}=\frac{1}{5}\end{cases}}\)
\(< =>\hept{\begin{cases}5.x=1.3\\y.5=1.2\end{cases}< =>\hept{\begin{cases}5x=3\\5y=2\end{cases}< =>\hept{\begin{cases}x=\frac{3}{5}\\y=\frac{2}{5}\end{cases}}}}\)
a) Ta có :\(\hept{\begin{cases}\left|x-1\right|\ge0\forall x\\\left|2x-y+3\right|\ge0\forall x;y\end{cases}}\Rightarrow\left|x-1\right|+\left|2x-y+3\right|\ge0\forall x;y\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x-1=0\\2x-y+3=0\end{cases}}\Rightarrow\hept{\begin{cases}x=1\\2x-y=-3\end{cases}}\Rightarrow\hept{\begin{cases}x=1\\y=5\end{cases}}\)
b) Ta có \(\hept{\begin{cases}\left|x-y\right|\ge0\forall x;y\\\left|x+y-2\right|\ge0\forall x;y\end{cases}\Rightarrow\left|x-y\right|+\left|x+y-2\right|\ge0\forall x;y}\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x-y=0\\x+y-2=0\end{cases}}\Rightarrow\hept{\begin{cases}x=y\\x+y=2\end{cases}}\Rightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}\)
c) Ta có \(\hept{\begin{cases}\left|x+y-1\right|\ge0\forall x;y\\\left|2x-3y\right|\ge0\forall x;y\end{cases}}\Rightarrow\left|x+y-1\right|+\left|2x-3y\right|\ge0\forall x;y\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x+y-1=0\\2x-3y=0\end{cases}}\Rightarrow\hept{\begin{cases}x+y=1\\2x=3y\end{cases}}\Rightarrow\hept{\begin{cases}x+y=1\\x=\frac{3}{2}y\end{cases}}\Rightarrow\hept{\begin{cases}x=\frac{3}{5}\\y=\frac{2}{5}\end{cases}}\)

Dấu hiệu là số lượng hsinh nữ trong 1 trường THCS
Có 30GT
| GT(x) | 6 | 12 | 14 | 16 | 18 | 17 | 19 | 20 | 13 | 10 15 25 |
| Tần số (n) | 1 | 2 | 3 | 5 | 3 | 4 | 3 | 3 | 1 | 1 3 1. N= 30 |
Có 12 GT khác nhau
Giá trị có tần số lớn(nhỏ) nhất là 16(6;13;10;25)
Mốt của dấu hiệu 14 --> 17
a) dấu hiệu cần tìm là : số lượng học sinh nữ của mỗi lớp
- Dấu hiệu đó có tất cả 30 giá trị
b) bảng tần số giờ ko lập dc ở đây



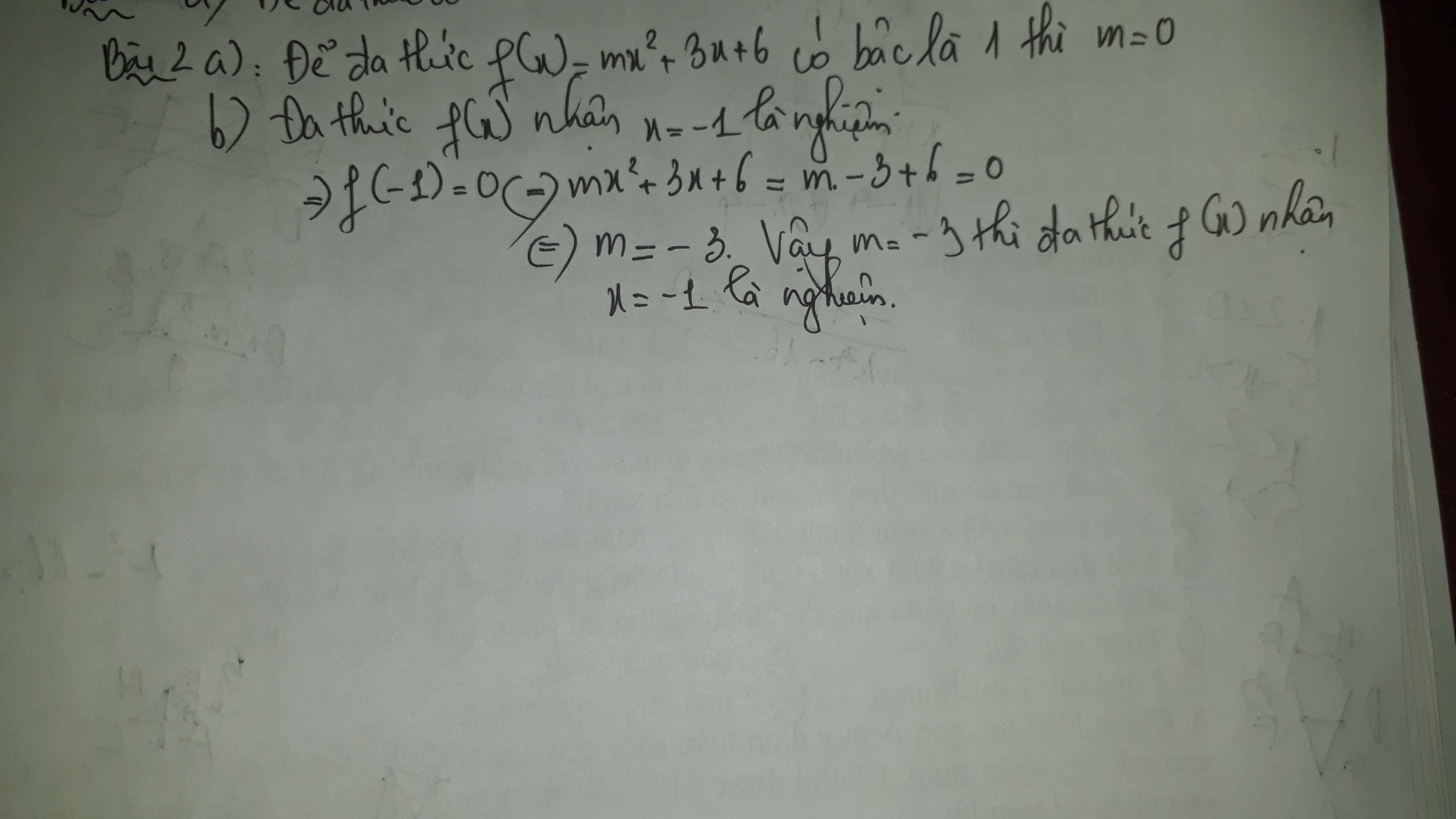



\(3.5^n=375\)
\(\Leftrightarrow5^n=375:3\)
\(\Leftrightarrow5^n=125=5^3\)
vậy \(n=3\)
hok tốt
\(3.5^n=375\)
\(\Rightarrow5^n=375:3\)
\(\Rightarrow5^n=125=5^3\)
\(\Rightarrow n=3\)