K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
10
D
1
23 tháng 5 2022
Thay \(x=2-\sqrt{3}\) vào Pt, ta được:
\(\left(2-\sqrt{3}\right)^2-3\left(2-\sqrt{3}\right)+k-1=0\)
\(\Leftrightarrow7-4\sqrt{3}-6+3\sqrt{3}+k-1=0\)
\(\Leftrightarrow k-\sqrt{3}=0\)
hay \(k=\sqrt{3}\)
\(x_1+x_2=3\)
nên \(x_2=3-2+\sqrt{3}=\sqrt{3}+1\)
AH
Akai Haruma
Giáo viên
17 tháng 1 2023
Lời giải:
PT có nghiệm $x=-2$
$\Leftrightarrow k(-2)^2+2(-2)-k+5=0$
$\Leftrightarrow 4k-4-k+5=0$
$\Leftrightarrow 3k+1=0$
$\Leftrightarrow k=\frac{-1}{3}$
Khi đó, pt trở thành:
$\frac{-1}{3}x^2+2x+\frac{16}{3}=0$
$\Leftrightarrow x^2-6x-16=0$
$\Leftrightarrow (x-8)(x+2)=0$
Do đó nghiệm còn lại là $x=8$
I
0
PP
2
NN
1
TA
5 tháng 8 2021
ĐK: `x>=0`.
`2\sqrt(20x)-2\sqrt(45x)+3/5 \sqrt(125x)=10`
`<=> 4\sqrt(5x) -6\sqrt(5x) +3\sqrt(5x)=10`
`<=>\sqrt(5x)=10`
`<=>5x=100`
`<=>x=25` (TM)
Vậy `S={25}`.
5 tháng 8 2021
bạn ơi có thể giải thích cho mình hiểu tại sao ĐKXĐ lại\(\ge\) 0 được k ạ
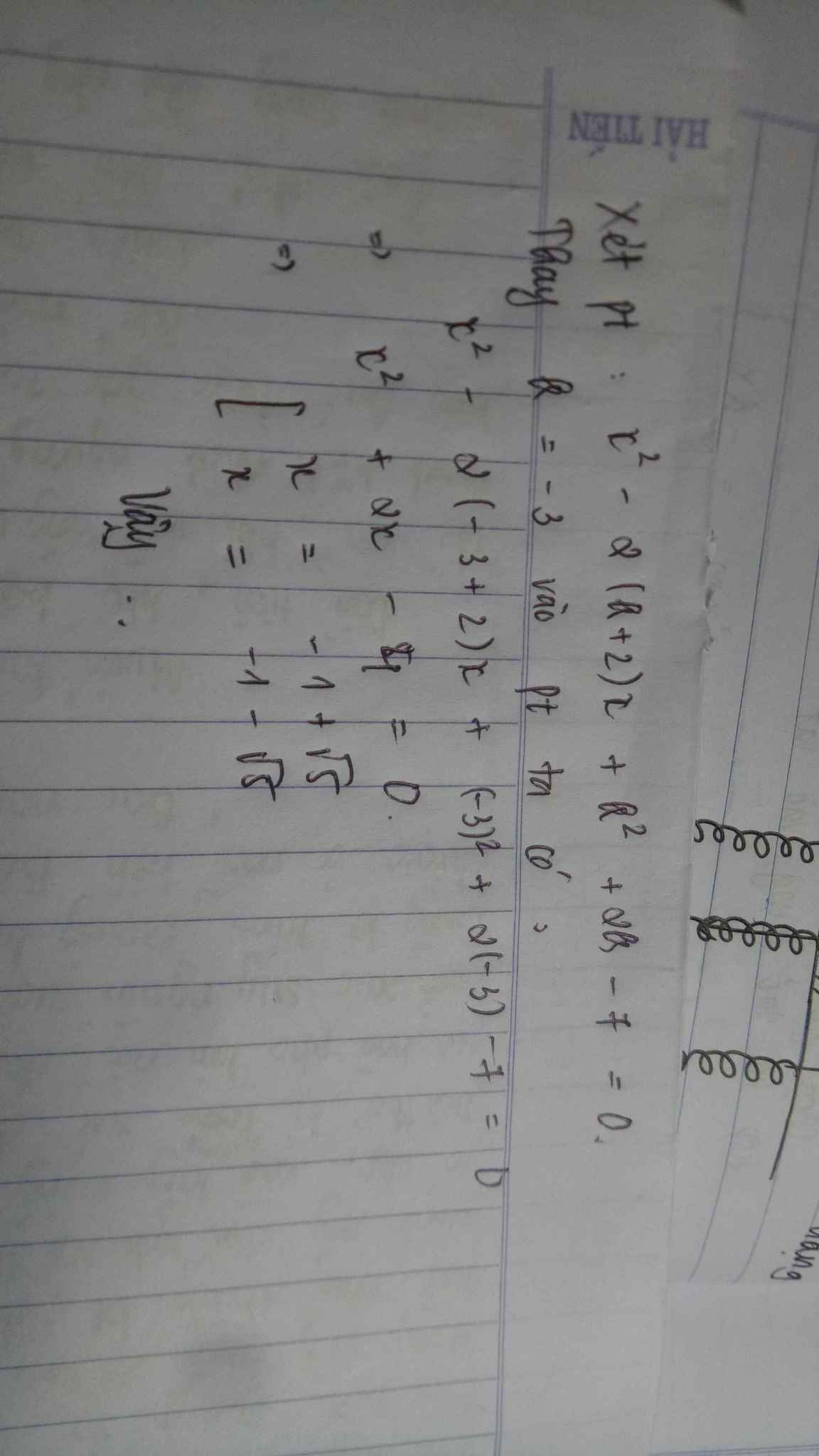
Đáp án là 10
Ai k mình2 k lại
2+2+2+2+2=2 x 5=10