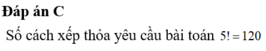Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Gọi A là biến cố: Xếp hai học sinh A, B ngồi ở hai bàn xếp cạnh nhau.
Số cách xếp ngẫu nhiên học sinh vào 36 cái bàn là 36!, ![]()
Ta tìm số cách xếp thuận lợi cho biến cố :
- Chọn 1 hàng hoặc 1 cột có C 12 1 cách;
- Mỗi hàng hoặc cột đều có 6 bàn nên có 5 cặp bàn xếp kề nhau, chọn lấy 1 trong 5 cặp bàn cạnh nhau trong hàng hoặc cột vừa chọn ra có C 5 1 cách;
- Xếp A và B vào cặp bàn vừa chọn có 2! cách;
- Xếp 34 học sinh còn lại có 34! cách.
Vậy tổng số cách xếp thoả mãn là: ![]()
Vậy xác suất cần tính: 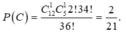

xếp ngẫu nhiên 8 bạn học sinh vào 4 bàn có 8! cách 40320 cách
=> \(n\left(\Omega\right)=40320\)
Gọi A:" có đúng 2 bàn mà trong đó mỗi bàn gồm 1 nam và 1 nữ "
=> \(n\left(A\right)=C^1_4.C^1_4..4.C^1_3.C^1_3.3.C^2_2.2.C^2_2.1=3456\) cách
=> P(A)= 3456/40320 =3/35

Xếp 6 học sinh trường A vào 1 dãy ghế: 6! cách
Xếp 6 học sinh trường B vào dãy còn lại: 6! cách
Lúc này hai học sinh đối diện luôn khác trường, có 6 cặp như vậy, mỗi cặp có 2 cách hoán vị nên có \(2^6\) cách hoán vị
Tổng cộng: \(6!.6!.2^6\) cách xếp thỏa mãn

a) Có 2 cách xếp.
Bạn A có 6! cách.
Bạn B có 6! cách.
Đổi vị trí A,B có tất cả 2*(6!)2 cách xếp chỗ.
b) Chọn 1 học sinh A vào vị trí bất kì: 12 cách.
Chọn 1 học sinh B đối diện A có 6 cách.
Cứ chọn liên tục như vậy ta được:
\(\left(12\cdot6\right)\cdot\left(10\cdot5\right)\cdot\left(8\cdot4\right)\cdot\left(6\cdot3\right)\cdot\left(4\cdot2\right)\cdot\left(2\cdot1\right)=2^6\cdot\left(6!\right)^2\)
cách xếp chỗ để hai bạn ngồi đối diện thì kkhasc trường nhau.

+ Số cách xếp 8 học sinh nói trên ngồi xung quanh một bạn tròn là 7 !.
+ Đếm số cách xếp 8 học sinh ngồi xung quanh một bàn tròn mà hai học sinh Hải và Liên ngồi cạnh nhau:
Trước tiên, số cách xếp 7 học sinh (trừ bạn Hải sẽ xếp sau) ngồi xung quanh một bàn tròn là 6 !
Khi đó có 2 cách xếp chỗ ngồi cho bạn Hải (ở bên trái hoặc bên phải bạn Liên).
Theo quy tắc nhân, sẽ có 6!.2 cách xếp 8 bạn ngồi xung quanh một bàn tròn mà hai bạn Hải và Liên ngồi cạnh nhau.
Vậy số cách xếp chỗ ngồi sao cho Hải và Liên không ngồi cạnh nhau là: 7! – 6!.2 =6!.5.
Chọn C.