Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xếp 6 học sinh trường A vào 1 dãy ghế: 6! cách
Xếp 6 học sinh trường B vào dãy còn lại: 6! cách
Lúc này hai học sinh đối diện luôn khác trường, có 6 cặp như vậy, mỗi cặp có 2 cách hoán vị nên có \(2^6\) cách hoán vị
Tổng cộng: \(6!.6!.2^6\) cách xếp thỏa mãn

Chọn C
![]()
Ta có số phần tử không gian mẫu: Ω = 10!.
+) Có 10 cách chọn học sinh cho vị trí số 1. Với mỗi cách chọn vị trí số 1 có 5 cách chọn học sinh cho vị trí số 10 ( Nếu vị trí số 1 là học sinh X thì có 5 cách chọn học sinh ở vị trí 10 là học sinh Y và ngược lại).
+) Có 8 cách chọn học sinh cho vị trí số 2 ( Loại 2 học sinh ở vị trí 10) . Với mỗi cách chọn vị trí số 2 có 4 cách chọn học sinh cho vị trí số 9( Nếu vị trí số 2 là X thì có 4 cách chọn vị trí số 9 là Y, chỉ còn 4 do đã loại 1 em ở lần chọn trước).
+) Hoàn toàn tương tự cho đến hết ta được số phần tử của biến cố cần tính xác suất là: ![]()
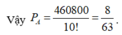

Chọn D
Cách 1. Xếp ngẫu nhiên 10 học sinh vào hai dãy ghế có cách.
Đánh số ghế lần lượt từ 1 đến 10.
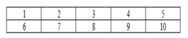
Xếp học sinh thỏa mãn bài toán xảy ra hai khả năng sau:
Khả năng 1: Nam ngồi vị trí lẻ, nữ ngồi vị trí chẵn có 5!.5! cách.
Khả năng 2: Nam ngồi vị trí chẵn, nữ ngồi vị trí lẻ có 5!.5! cách.
Vậy có tất cả 2. ( 5 ! ) 2 cách.
Xác suất cần tìm bằng 
Cách 2: Xếp ngẫu nhiên 10 học sinh vào hai dãy ghế, có 10! cách xếp.
Ta chia hai dãy ghế thành 5 cặp ghế đối diện:
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 1 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 2 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 3 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 4 có ![]() cách;
cách;
+ Chọn 1 nam và 1 nữ xếp vào cặp ghế 5 có 1 cách.
Vậy có tất cả ![]() cách xếp thỏa mãn.
cách xếp thỏa mãn.
Xác suất cần tìm bằng 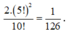

Đánh số 10 vị trí ngồi từ 1 đến 10 trong đó 1 đến 5 là hàng 1 thuộc bàn 1, còn 6 đến 10 là hàng 2 thuộc bàn 2.
Giả sử 1 học sinh trường X ngồi vị trí số 1, thì các học sinh còn lại của trường X chỉ ngồi ở vị trí số lẻ, còn 5 học sinh của trường Y chỉ ngồi vị trí số chẵn.
Số cách xếp lúc này là: 5!.5!. Tương tự với trường hợp học sinh trường X ngồi vị trí số chẵn.
vậy số cách xếp cần tìm: 2.5!.5! = 28800.
Chọn D.

Đáp án A
Xếp 12 học sinh vào 12 ghế có 12! Cách
![]()
Xếp chỗ ngồi cho 2 nhóm học sinh nam – nữ có 2 cách
Trong nhóm có học sinh nam, có 6! Cách sắp xếp 6 học sinh vào 6 chỗ ngồi
Trong nhóm có học sinh nữ, có 6! Cách sắp xếp 6 học sinh vào 6 chỗ ngồi
Suy ra có ![]() cách xếp thỏa mãn bài toán.
cách xếp thỏa mãn bài toán.
Vậy ![]()

Chọn A.
Số phần tử của không gian mẫu là n(W =) 6!.
Gọi A là biến cố : "Các bạn học sinh nam ngồi đối diện các bạn nữ".
Chọn chỗ cho học sinh nam thứ nhất có 6 cách.
Chọn chỗ cho học sinh nam thứ 2 có 4 cách (không ngồi đối diện học sinh nam thứ nhất)
Chọn chỗ cho học sinh nam thứ 3 có 2 cách (không ngồi đối diện học sinh nam thứ nhất, thứ hai).
Xếp chỗ cho 3 học sinh nữ : 3! cách.
Theo quy tắc nhân ta có cách
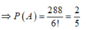





a) Có 2 cách xếp.
Bạn A có 6! cách.
Bạn B có 6! cách.
Đổi vị trí A,B có tất cả 2*(6!)2 cách xếp chỗ.
b) Chọn 1 học sinh A vào vị trí bất kì: 12 cách.
Chọn 1 học sinh B đối diện A có 6 cách.
Cứ chọn liên tục như vậy ta được:
\(\left(12\cdot6\right)\cdot\left(10\cdot5\right)\cdot\left(8\cdot4\right)\cdot\left(6\cdot3\right)\cdot\left(4\cdot2\right)\cdot\left(2\cdot1\right)=2^6\cdot\left(6!\right)^2\)
cách xếp chỗ để hai bạn ngồi đối diện thì kkhasc trường nhau.
Ở ý a) tại sao bạn A lại có $6!$ cách v ạ?
bạn B cx thế ạ?