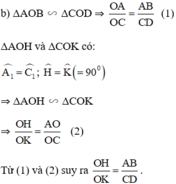Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Xét ∆ABC và ∆KBA có :
B là góc chung
BAC = BKA
=> ∆ ABC ĐỒNG DẠNG với ∆KBA
=>BA TRên KB = BC TRÊN BA
=>AB²= BK.BC
https://h.vn/hoi-dap/question/585511.html
Bạn xem cả bài ở link này đi(mik gửi cho)
Học tôt!!!!!!!!!!!!

c. -Xét △ADC có: OM//DC (gt).
\(\Rightarrow\dfrac{MO}{DC}=\dfrac{AO}{AC}\) (định lí Ta-let).
\(\Rightarrow\dfrac{DC}{MO}=\dfrac{AC}{AO}\)
\(\Rightarrow\dfrac{DC}{OM}-1=\dfrac{OC}{AO}\) (1).
-Xét △BDC có: ON//DC (gt).
\(\Rightarrow\dfrac{ON}{DC}=\dfrac{BO}{BD}\) (định lí Ta-let).
\(\Rightarrow\dfrac{DC}{ON}=\dfrac{BD}{BO}\)
\(\Rightarrow\dfrac{DC}{ON}-1=\dfrac{OD}{BO}\)
-Xét △ABO có: AB//DC (gt).
\(\Rightarrow\dfrac{OD}{BO}=\dfrac{OC}{OA}=\dfrac{DC}{AB}\) (3)
-Từ (1), (2),(3) suy ra:
\(\dfrac{DC}{OM}-1=\dfrac{DC}{ON}-1=\dfrac{DC}{AB}\)
\(\Rightarrow\dfrac{DC}{OM}=\dfrac{DC}{ON}=\dfrac{DC}{AB}+1=\dfrac{AB+DC}{AB}\)
\(\Rightarrow\dfrac{1}{OM}=\dfrac{1}{ON}=\dfrac{AB+DC}{AB.DC}=\dfrac{1}{AB}+\dfrac{1}{CD}\)
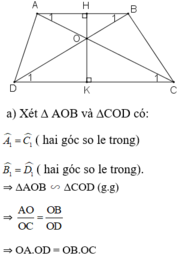
a: Xét ΔAOB và ΔCOD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó: ΔAOB∼ΔCOD
Suy ra: \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}\)
hay \(OA\cdot OD=OB\cdot OC\)
b: \(\dfrac{OA}{OC}=\dfrac{AB}{CD}\)
\(\Leftrightarrow OA=\dfrac{1}{2}\cdot6=3\left(cm\right)\)

a: Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng vơi ΔOCD
=>OA/OC=OB/OD=AB/CD
=>OA*OD=OB*OC
b: OA/OC=AB/CD
=>OA/6=5/10=1/2
=>OA=3cm
Xet ΔADC có OE//DC
nên OE/DC=AO/AC
=>OE/10=3/(3+6)=3/9=1/3
=>OE=10/3cm

a) Xét \(\Delta OAB\)và \(\Delta OCD\)có:
\(\widehat{OAB}=\widehat{OCD}\) (slt)
\(\widehat{OBA}=\widehat{ODC}\) (slt)
suy ra: \(\Delta OAB~\Delta OCD\) (g.g)
\(\Rightarrow\)\(\frac{OA}{OC}=\frac{OB}{OD}\)
\(\Rightarrow\)\(OA.OD=OB.OC\)
b) \(\Delta OAB~\Delta OCD\)
\(\Rightarrow\)\(\frac{OA}{AC}=\frac{AB}{CD}\)
\(\Rightarrow\)\(OA=\frac{OC.AB}{CD}=3\)
\(\Rightarrow\)\(AC=OA+OC=9\)
\(\Delta AEO~\Delta ADC\) ( do OE // DC )
\(\Rightarrow\)\(\frac{OE}{DC}=\frac{OA}{AC}\) \(\Rightarrow\) \(OE=\frac{OA.DC}{AC}=\frac{10}{3}\)