Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

11.3
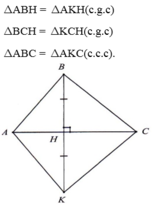
Xét ΔABH vuông tại H và ΔKBH vuông tại H có
HB chung
HA=HK
Do đó; ΔABH=ΔKBH
Xét ΔACH vuông tại H và ΔKCH vuông tại H có
HC chung
HA=HK
Do đo: ΔACH=ΔKCH
Xét ΔABC và ΔKBC có
BA=BK
BC chung
AC=KC
Do đó: ΔABC=ΔKBC

các cặp tam giác bằng nhau là
ACH=CHK
ABH=HBK
ABC=BCK
ACK=ABK(nó chỉ đúng khi góc B và góc C của tam giác ABC có số đo góc bằng nhau)

Xét tam giác AOM và tam giác BOM có:
AO = BO (gt)
AOM = BOM (OM là tia phân giác của AOB)
OM chung
=> Tam giác AOM = Tam giác BOM (c.g.c)
=> AM = BM (2 cạnh tương ứng)
=> M là trung điểm của AB
=> OM là đường trung tuyến của tam giác OAB cân tại O (OA = OB)
=> OM là đường trung trực của tam giác OAB cân tại O
=> OM _I_ AB
Tam giác NAB có NA vừa là đường cao, vừa là đường trung trực
=> Tam giác NAB cân tại N
=> NA = NB

xét tam giác ABE và tam giác ADE
AE chung
góc BAE = góc DAE(AE la tia phân giác của góc E)
AB = AD ( gt)
=> tam giác ABE = tam giac DAE ( c.g.c)
b) xét tam giác ABI và tam giác ADI
AI chung
góc BAE = góc DAE
tam giác ABI=tam giác ADI
=> BI = DI ( 2 cạnh t/ứ )
=> I là trung điểm của BD