
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c, \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
<=> \(C=\left(2\sqrt{3}-15\sqrt{3}+8\sqrt{3}\right):\sqrt{3}\)
<=> \(C=-5\sqrt{3}:\sqrt{3}=-5\)
e. \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\sqrt{9-5}\)
\(=6+4=10\)
b. \(\left(\sqrt{3}+2\right)^2-\sqrt{75}\)
\(=3+4\sqrt{3}+4-5\sqrt{3}\)
\(=7-\sqrt{3}\)
d. \(\left(1+\sqrt{3}-\sqrt{2}\right)\left(1+\sqrt{3}+\sqrt{2}\right)\)
\(=\left(1+\sqrt{3}\right)^2-2\)
\(=1+2\sqrt{3}+3-2\)
\(=2+2\sqrt{3}\)
f. \(\sqrt{\left(\sqrt{3}+2\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\left|\sqrt{3}+2\right|-\left|\sqrt{3}-2\right|\)
\(=\sqrt{3}+2-2+\sqrt{3}\)
\(=2\sqrt{3}\)
c: Ta có: \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-5\cdot3\sqrt{3}+4\cdot2\sqrt{3}\right):\sqrt{3}\)
\(=2-15+8=-5\)
d: Ta có: \(D=\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\cdot2=10\)

1.2 với \(x\ge0,x\in Z\)
A=\(\dfrac{2\sqrt{x}+7}{\sqrt{x}+2}=2+\dfrac{3}{\sqrt{x}+2}\in Z< =>\sqrt{x}+2\inƯ\left(3\right)=\left(\pm1;\pm3\right)\)
*\(\sqrt{x}+2=1=>\sqrt{x}=-1\)(vô lí)
*\(\sqrt{x}+2=-1=>\sqrt{x}=-3\)(vô lí
*\(\sqrt{x}+2=3=>x=1\)(TM)
*\(\sqrt{x}+2=-3=\sqrt{x}=-5\)(vô lí)
vậy x=1 thì A\(\in Z\)


Lời giải:
Từ ĐKĐB suy ra:
$-x^2+5xy+2y^2=3(x^2+y^2)$
$\Leftrightarrow 4x^2-5xy+y^2=0$
$\Leftrightarrow 4x(x-y)-y(x-y)=0$
$\Leftrightarrow (4x-y)(x-y)=0$
$\Rightarrow 4x=y$ hoặc $x=y$.
Nếu $4x=y$. Thay vô PT $(1)$ thì:
$x^2+(4x)^2=1\Rightarrow x=\pm \frac{1}{\sqrt{17}}$
$\Rightarrow x=\pm \frac{4}{\sqrt{17}}$ (tương ứng)
Trường hợp $x=y$ tương tự, ta tìm được $(x,y)=(\pm \frac{1}{\sqrt{2}}; \pm \frac{1}{\sqrt{2}})$

\(\sqrt{4x-8}-\sqrt{x-2}=2.\)
ĐK \(x\ge2\)
PT<=> \(2\sqrt{x-2}-\sqrt{x-2}=2\)
<=> \(\sqrt{x-2}=2\)
<=> x-2=4
<=> x=6 (t/m)
Vậ pt có nghiệm x=6

\(3\sqrt{2a}-\sqrt{2.3^2a.a^2}-\frac{1}{4}\sqrt{8^2.2a}=3\sqrt{2a}-3a\sqrt{2a}-2\sqrt{2a}=\sqrt{2a}-3a\sqrt{2a}\)
\(\left(1-3a\right)\sqrt{2a}\)
nếu là phương trình :
\(\sqrt{2a}\left(1-3a\right)=0\Leftrightarrow\left(1-3a\right)=0\Leftrightarrow1-3a=0\Leftrightarrow a=\frac{1}{3}\)
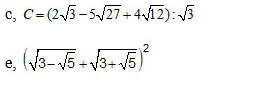
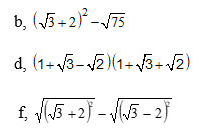 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp

`sqrt{1-x}>5`
`đk:x<=1`
`bpt<=>1-x>25`
`<=>x<1-25=-24`
Vậy BPT có tập nghiệm `S={x|x<-24}`
\(\sqrt{1-x}>5\left(ĐK:x\le1\right)\\ \Leftrightarrow1-x>25\\ \Leftrightarrow-x>24\\ \Leftrightarrow x< -24\)
Vậy \(S=\left\{x|x< -24\right\}\) là tập nghiệm của bất phương trình