T
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
XT
1
1 tháng 4 2022
\(x+2y=6\)
\(\Leftrightarrow\dfrac{6}{2}=\dfrac{x}{2}+y\)
\(P+\dfrac{6}{2}=\dfrac{8}{x}+\dfrac{1}{y}+\dfrac{x}{2}+y\)
\(\Leftrightarrow P+\dfrac{6}{2}=\left(\dfrac{8}{x}+\dfrac{1}{y}\right)+\left(\dfrac{1}{y}+y\right)\)
vì x;y là số thực dương ,áp dụng BĐT Côsi ta có :
\(\dfrac{8}{x}+\dfrac{x}{2}=2\sqrt{\dfrac{8}{x}+\dfrac{x}{2}}=2\sqrt{4}=2.2=4\)
\(\dfrac{1}{y}+y=2\sqrt{\dfrac{1}{y}+y}=2\sqrt{1}=2.1=2\)
nên \(P+\dfrac{6}{2}\ge6\)
\(\Leftrightarrow P\ge6-\dfrac{6}{2}\)
\(\Leftrightarrow P\ge3\)
vậy \(P_{min}=3\)
HN
1
13 tháng 4 2022
We have : \(A=x+y+\dfrac{1}{2x}+\dfrac{2}{y}=\dfrac{x+y}{2}+\left(\dfrac{y}{2}+\dfrac{2}{y}\right)+\left(\dfrac{1}{2x}+\dfrac{x}{2}\right)\)
\(Applying\) C-S we have : \(\dfrac{y}{2}+\dfrac{2}{y}\ge2;\dfrac{1}{2x}+\dfrac{x}{2}\ge1\)
x + y \(\ge3\) \(\Rightarrow\dfrac{x+y}{2}\ge\dfrac{3}{2}\)
So : \(A\ge\dfrac{3}{2}+2+1=\dfrac{9}{2}\)
" = " \(\Leftrightarrow x=1;y=2\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 3 2021
\(B=\dfrac{1}{x^3+y^3}+\dfrac{1}{xy\left(x+y\right)}=\dfrac{1}{x^3+y^3}+\dfrac{3}{3xy\left(x+y\right)}\)
\(B\ge\dfrac{\left(1+\sqrt{3}\right)^2}{x^3+y^3+3xy\left(x+y\right)}=\dfrac{4+2\sqrt{3}}{\left(x+y\right)^3}=4+2\sqrt{3}\)
\(B_{min}=4+2\sqrt{3}\) khi \(\left(x;y\right)=\left(\dfrac{3+\sqrt{3}-\sqrt[4]{12}}{6+2\sqrt{3}};\dfrac{3+\sqrt{3}+\sqrt[4]{12}}{6+2\sqrt{3}}\right)\) và hoán vị
AH
Akai Haruma
Giáo viên
12 tháng 3 2021
Lời giải:
Áp dụng BĐT Cauchy-Shwarz:
$B=\frac{1}{x^3+y^3}+\frac{1}{xy}=\frac{1}{(x+y)^3-3xy(x+y)}+\frac{1}{xy}$
$=\frac{1}{1-3xy}+\frac{1}{xy}=\frac{1}{1-3xy}+\frac{3}{3xy}$
$\geq \frac{(1+\sqrt{3})^2}{1-3xy+3xy}=(1+\sqrt{3})^2$
Vậy $B_{\min}=(1+\sqrt{3})^2$
Dấu "=" xảy ra khi $xy=\frac{1}{2}-\frac{1}{2\sqrt{3}}$
DD
Đoàn Đức Hà
Giáo viên
21 tháng 6 2021
Ta có bất đẳng thức: với \(x,y>0\)
\(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
Dấu \(=\)khi \(x=y\).
Áp dụng bất đẳng thức trên ta được:
\(\frac{1}{2x+3y+3z}\le\frac{1}{4}\left(\frac{1}{2x+y+z}+\frac{1}{2y+2z}\right)\le\frac{1}{4}\left[\frac{1}{4}\left(\frac{1}{x+y}+\frac{1}{x+z}\right)+\frac{1}{2}\left(\frac{1}{y+z}\right)\right]\)
\(=\frac{1}{16}\left(\frac{1}{x+y}+\frac{1}{x+z}\right)+\frac{1}{8}\left(\frac{1}{y+z}\right)\)
Tương tự với \(\frac{1}{3x+2y+3z},\frac{1}{3x+3y+2z}\)sau đó cộng lại vế với vế ta được:
\(P\le\frac{1}{4}\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)=3\)
Dấu \(=\)xảy ra khi \(x=y=z=\frac{1}{8}\)
HP
16 tháng 1 2021
Áp dụng BĐT BSC:
\(F=\dfrac{1}{2x+y+z}+\dfrac{1}{x+2y+z}+\dfrac{1}{x+y+2z}\)
\(\le\dfrac{1}{16}\left(\dfrac{1}{x}+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)+\dfrac{1}{16}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{y}+\dfrac{1}{z}\right)+\dfrac{1}{16}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+\dfrac{1}{z}\right)\)
\(=\dfrac{1}{16}\left(\dfrac{4}{x}+\dfrac{4}{y}+\dfrac{4}{z}\right)=\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)=\dfrac{1}{4}.4=1\)
\(maxF=1\Leftrightarrow x=y=z=\dfrac{3}{4}\)
PT
1
CM
26 tháng 6 2019
Vì
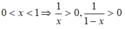
Áp dụng bất đẳng thức Cô – si đối với hai số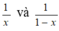 
ta được:
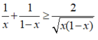
Vì 0 < x < 1 ⇒ 1 - x > 0
Áp dụng bất đẳng thức Cô – si đối với hai số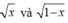 
ta được:
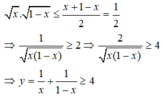
Dấu “ = ” xảy khi và chỉ khi
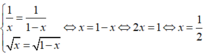
Vậy giá trị nhỏ nhất của hàm số bằng 4 tại x = 1/2
Sửa: \(P=2x^4+x^3\left(2y-1\right)+y^3\left(2x-1\right)+2y^4\); x+y=1
Ta có \(P=2x^4+x^3\left(2y-1\right)+y^3\left(2x-1\right)+2y^4=2x^4+2x^3y-x^3+2xy^3-y^3+2y^4\)
\(=x^3\left(2x+2y\right)+y^3\left(2x+2y\right)-\left(x^3+y^3\right)=\left(2x+2y\right)\left(x^3+y^3\right)-\left(x^3+y^3\right)\)
\(=\left(2x+2y-1\right)\left(x^3+y^3\right)=x^3+y^3\)
Do \(x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=x^2-xy+y^2=\frac{1}{2}\left(x^2+y^2\right)\left(\frac{x}{\sqrt{2}}-\frac{y}{\sqrt{2}}\right)^2\)
\(\Rightarrow P\ge\frac{1}{2}\left(x^2+y^2\right)\)
Mà \(x+y=1\Rightarrow x^2+y^2+2xy=1\Rightarrow2\left(x^2+y^2\right)-\left(x-y\right)^2=1\)
\(\Rightarrow2\left(x^2+y^2\right)\ge1\Rightarrow\left(x^2+y^2\right)\ge\frac{1}{2}\Rightarrow P\ge\frac{1}{4}\)
Dấu "=" xảy ra khi \(x=y=\frac{1}{2}\)