Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi 2 số đó là a và b (a\(\ge0,b\ge0\) )
câu a
Áp dụng BĐT Bu-nhia -xkop-ki ,ta có
a+b\(\le\sqrt{\left(a^2+b^2\right)\left(1^2+1^2\right)}\)
\(\Leftrightarrow82\le\sqrt{\left(a^2+b^2\right)2}\) \(\Rightarrow\) \(6724\le\left(a^2+b^2\right)2\Leftrightarrow\left(a^2+b^2\right)\ge3362\)
Vậy Min a2+b2=3362\(\Leftrightarrow a=b=41\)
Gọi số thứ nhất là a; số thứ hai là b
Ta có 1/3*a-b=1
=> 1/3*a=b+1
=> a=(b+1):1/3
=> a=(b+1)*3
Mà a+b=43
Hay (b+1)*3+b=43
<=> 3b+3+b=43
<=> 4b+3=43
<=> 4b=43-3
<=> 4b=40
=> b=40:4
=> b=10
=>a=(10+1)*3
=>a=11*3
=>a=33
Vậy số thứ nhất là 33;số thứ 2 là 10
Ta đặt A = 1 + 2 + 3 + 4 + 5 + ... + 49 + 50.
Dãy số tự nhiên liên tiếp từ 1 đến 50 có 50 số, trong đó số các số lẻ bằng số các số chẵn nên có 50 : 2 = 25 (số lẻ).
Vậy A là một số lẻ.
Gọi a và b là hai số bất kì của A, khi thay tổng a + b bằng hiệu a - b thì A giảm đi :
(a + b) - (a - b) = 2 x b
Tức là giảm đi một số chẵn. Hiệu của một số lẻ và một số chẵn luôn là một số lẻ nên sau mỗi lần thay, tổng mới vẫn là một số lẻ.
Vì vậy không bao giờ nhận được kết quả là 0
Ta đặt A = 1 + 2 + 3 + 4 + 5 + ... + 49 + 50.
Dãy số tự nhiên liên tiếp từ 1 đến 50 có 50 số, trong đó số các số lẻ bằng số các số chẵn nên có 50 : 2 = 25 (số lẻ). Vậy A là một số lẻ. Gọi a và b là hai số bất kì của A, khi thay tổng a + b bằng hiệu a - b thì A giảm đi : (a + b) - (a - b) = 2 x b tức là giảm đi một số chẵn. Hiệu của một số lẻ và một số chẵn luôn là một số lẻ nên sau mỗi lần thay, tổng mới vẫn là một số lẻ. Vì vậy không bao giờ nhận được kết quả là 0
a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 - 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
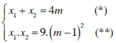
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
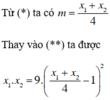
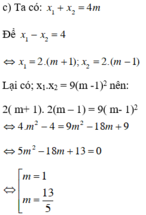
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành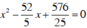 
có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.
Nếu có P => Q thì ta gọi P là điều kiện cần của Q và đồng thời Q cũng là điều kiện đủ của P
Ta gọi mệnh đề P : a và b - chúng đều là 2 số hữu tỉ, Q : tổng a + b là số hữu tỉ
Mệnh đề ở gt : P => Q
Mệnh đề A : P => Q
Mệnh đề B : Q => P
Mệnh đề C : Q => P
Mệnh đề D : A,B,C đều sai
=> Do đó chúng ta chọn đáp án A là hợp lí nhất.
