Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Xếp ngẫu nhiên 7 tấm bìa có ![]() (cách xếp)
(cách xếp)
![]()
Đặt A là biến cố “xếp được chữ HIỀN TÀI LÀ NGUYÊN KHÍ QUỐC GIA”.
Ta có ![]()
Vậy ![]()

Đáp án D
Sắp sếp 8 chữ cái trong cụm từ THANHHOA có ![]() cách sắp xếp (vì có 3 chữ H giống nhau)
cách sắp xếp (vì có 3 chữ H giống nhau)
Gọi A là biến cố “có ít nhất hai chữ cái H đứng cạnh nhau”
Suy ra ![]() là biến cố “không có hai chữ cái H nào đứng cạnh nhau”
là biến cố “không có hai chữ cái H nào đứng cạnh nhau”
Trước hết ta sắpxếp 5 chữ cái T, A, N, O, A vào 5 vị trí khác nhau có 5! Cách sắp xếp, khi đó có ![]() cách chèn thêm 3 chữ cái H để dãu có 8 chữ cái
cách chèn thêm 3 chữ cái H để dãu có 8 chữ cái
Suy ra có ![]() cách.
cách.
Khi đó
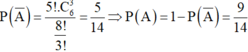

Đáp án C
Cách giải:
Xét các số x = a; y = b + 1; z = c + 2; t = d + 3. Vì 1 ≤ a ≤ b ≤ c ≤ d ≤ 9 => 1 ≤ x < y < z < t ≤ 12 (*)
Và mỗi bộ 4 số (x;y;z;t) được chọn từ tập hợp 1 ; 2 ; . . . . ; 12 ta đều thu được bộ số thỏa mãn (*). Do đó, số cách chọn 4 số trong 12 số là C 12 4 = 495 số suy ra n ( X ) = 495
Số phần tử của không gian mẫu là n ( Ω ) = 9 . 10 . 10 . 10 = 9000
Vậy xác suất cần tính là
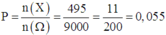

Chọn D
Chọn số tự nhiên có 4 chữ số bất kỳ có: ![]() (cách).
(cách).
Gọi A là biến cố: “Số được chọn có dạng a b c d ¯ , trong đó 1 ≤ a ≤ b ≤ c ≤ d ≤ 9” . (*)
Cách 1: Dùng tổ hợp
Nhận xét rằng với 2 số tự nhiên bất kỳ ta có: ![]()
Do đó nếu đặt:
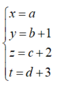
Từ giả thuyết ![]() ta suy ra:
ta suy ra: ![]()
Với mỗi tập con gồm 4 phần tử đôi một khác nhau được lấy ra từ {1,2,....,12}ta đều có được duy nhất một bộ số thoả mãn (**) và do đó tương ứng ta có duy nhất một bộ số (a,b,c,d) thoả mãn (*). Số cách chọn tập con thoả tính chất trên là tổ hợp chập 4 của 12 phần tử, do đó:
![]()
Vậy 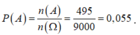
Cách 2: Dùng tổ hợp lặp
Chọn số tự nhiên có 4 chữ số bất kỳ có: ![]() (cách).
(cách).
Mỗi tập con có 4 phần tử được lấy từ tập {1,2,...,9}(trong đó mỗi phần tử có thể được chọn lặp lại nhiều lần) ta xác định được một thứ tự không giảm duy nhất và theo thứ tự đó ta có được một số tự nhiên có dạng
a
b
c
d
¯
(trong đó ![]() ). Số tập con thoả tính chất trên là số tổ hợp lặp chập 4 của 9 phần tử
). Số tập con thoả tính chất trên là số tổ hợp lặp chập 4 của 9 phần tử
Do đó theo công thức tổ hợp lặp ta có: ![]()
Vậy 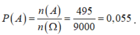
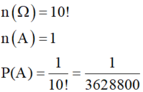


Xếp ngẫu nhiên 66 chữ cái : 6! = 720 cách
Nhưng vì trong đó có 2 cặp chữ cái giống nhau nên số cách thực sự là \(\frac{720}{2^2}=180\)
=> Xác suất để em đó trong khi xếp ngẫu nhiên thu được chữ NGHÊNH là : \(\frac{1}{180}\)
~Study well~