ngày THI ĐẤU OLM tối nay, ngày 28/04/2023 để so tài với học sinh toàn quốc!!!

Ôn tập kiểm tra học kì 2 hiệu quả, đạt thành tích cao!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
LT
Lê Thị Bích Tuyền
15 tháng 7 2015 - olm

Cho tam giác ABC có AB = AC , tia phân giác của góc A cắt BC tại D . Lấy điểm E trên cạnh AD .

a) C/m tam giác AEB = AEC

b) C/m ED là phân giác của góc BEC

   C/m AD vuông góc BC
#Toán lớp 7
1
BT
Bảo Trang
15 tháng 7 2015

 

A B C D E --

 

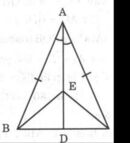
a) Xét hai tg AEB và AEC có 

AE cạnh chungg

BAD = CAD [ Tia phân giác của góc A ]

AB = AC [ gt ] 

=> tg AEB= AEC [ c - g c ]

b ) Tam giác ABC cân có AD là phân giác nên đồng thời là đường cao => AD vuông góc với BC

tg AEB = tg AEC  [ cmt ]

=> EB= EC => tg BEC cân tại B , có AD là đường cao nên đồng thời là phân giác => ED là phan giác góc BEC

Đúng(2)
TD
Trần Đại Vỹ
18 tháng 11 2016 - olm

Cho tam giác ABC có AB=AC, tia phân giác của góc A cắt cạnh BC tai D. Lấy E trên ED. CMR:

a) Tam giác AEB = tam giác AED

b) ED là tia phân giác của góc BEC ( 2 cách)

c) AD vuông góc với BC
#Toán lớp 7
1
NL
Nguyễn Lê Phước Thịnh
5 tháng 10 2022

a: Xét ΔAEB và ΔAEC có

AB=AC

góc BAE=góc CAE
AE chung

Do đó: ΔAEB=ΔAEC

b: Xét ΔEDB và ΔEDC có

ED chung

EB=EC

BD=CD

DO đó: ΔEDB=ΔEDC

=>góc BED=góc CED

=>ED là phân giác của góc BEC

c: Ta có: ΔABC cân tại A

mà AD là đường phân giác

nên AD là đường cao

Đúng(0)
DT
Đào Thị Lê Na
29 tháng 4 2017 - olm

Trong tam giác ABC vuông tại A có góc B = 60 độ

a, trên cạnh BC lấy điểm D sao cho BA= BD qua D vẽ đường vuông góc với BC cắt tia đối của tia AB tại E . C/M tam giác ABC và tam giác DBE

c, gọi H là giao điểm của ED và AD. C/m BH là tia phân giác của góc ABC

d, qua B vẽ đường vuông góc với AB cắt ED tại K . C/m tam giác HBK đều

e, AB+ AC -BC/2 < AD< AD+AC+BC/2

hép mi 
#Toán lớp 7
0
NH
Nguyễn Hoàng Khả Hân
25 tháng 8 2017 - olm
1) Cho tam giác ABC có AB<AC. Tia phân giác của góc A cắt BC ở D. Trên cạnh AC lấy một điểm E sao cho AE = ABa) C/m tam giác ABD = tam giác AEDb) C/m AD vuông góc với BEc) Chứng minh góc ADB < góc ADC2) Cho tam giác ABC có AB<AC, AD là tia phân giác của góc BAC ( D thuộc BC ). Trên cạnh AC lấy một điểm E sao cho AE = ABa) C/m tam giác ADB = tam giác ADEb) Gọi F là giao điểm của tia AB và tia ED. Chứng minh tam giác BFD = tam giác...
Đọc tiếp

1) Cho tam giác ABC có AB<AC. Tia phân giác của góc A cắt BC ở D. Trên cạnh AC lấy một điểm E sao cho AE = AB
a) C/m tam giác ABD = tam giác AED
b) C/m AD vuông góc với BE
c) Chứng minh góc ADB < góc ADC

2) Cho tam giác ABC có AB<AC, AD là tia phân giác của góc BAC ( D thuộc BC ). Trên cạnh AC lấy một điểm E sao cho AE = AB
a) C/m tam giác ADB = tam giác ADE
b) Gọi F là giao điểm của tia AB và tia ED. Chứng minh tam giác BFD = tam giác ECD
c) So sánh DB và DC
#Toán lớp 7
0
LQ
Lê Quốc Hùng
19 tháng 12 2016 - olm

Cho tam giác ABC có AB = AC, tia phân giác của góc BAC cắt BC tại D
a) C/m: tam giác ABD = tam giác ACD. Từ đó suy ra AD vuông góc BC
b)kẻ BE vuông góc AC (E thuộc AC). TRên cạnh AB lấy điểm F sao cho AE = AF. C/m: tam giác AEB = tam giác AFC. Từ đó suy ra CF vuông góc AB.
c)BE cắt AD tại H. C/m: góc AFH = 90độ. Từ dó suy ra ba điểm C,H,F thẳng hàng.
d)C/m: DE = 1/2 BC
#Toán lớp 7
0
NL
Nguyễn Linh Na
24 tháng 7 2019 - olm

Cho tam giác ABC vuông góc tại  . Trên cạnh BC lấy điểm D sao cho BD=BA. Tia phân giác góc ABC cắt cạnh BC tại E.

a) C/m tam giác BAE = tam giác BDE

b) C/m ED vuông góc với BC

c) C/m AE= DE

d) Trên tia đối của tia AB lấy điểm I sao cho AI= DC. C/m tam giác AEI= tam giác DEC. Từ đó c/m ba điểm D,E,I thẳng hàng.
#Toán lớp 7
1
JK
Jennie Kim
24 tháng 7 2019

A B C D E I O

a, xét tam giác BAE và tam giác BDE có : BE chung

góc ABE = góc DBE do BE là phân giác của góc ABC (gt)

AB = BD (gt)

=> tam giác BAE = tam giác BDE (c-g-c)

b, tam giác BAE = tam giác BDE (câu a)

=> góc BAE = góc BDE (đn)

mà óc BAE = 90 do tam giác ABC vuông tại A (gt)

=> góc BDE = 90 

=> ED _|_ BC (đn)

c, tam giác BAE = tam giác BDE (Câu a)

=> AE = DE (đn)

d,  gọi BE cắt CI tại O 

AB = BD (gt)

AI = DC (gt)

AB + AI = BI 

BD + DC = BC

=> BI = BC 

xét tam giác IOB và tam giác COB có : OB chung

góc IBO = góc CBO do BO là phân giác của góc IBC (gt)

=> tam giác IOB = tam giác COB (c-g-c)

=> góc IOB = góc COB (đn)

mà góc IOB + góc COB = 180 (kb)

=> góc IOB = 180 : 2 = 90 

=> BO _|_ CI (đn)

CA _|_ AB do góc BAC = 90 

xét tam giác IBC 

=> ID _|_ BC (tc)

mà ED _|_ BC (câu b)

=> I; E; D thẳng hàng

Đúng(0)
LQ
Lê Quốc Hùng
19 tháng 12 2016 - olm

Cho tam giác ABC có AB = AC, tia phân giác của góc BAC cắt BC tại D
a) C/m: tam giác ABD = tam giác ACD. Từ đó suy ra AD vuông góc BC
b)kẻ BE vuông góc AC (E \(\in\) AC). TRên cạnh AB lấy điểm F sao cho AE = AF. C/m: tam giác AEB = tam giác AFC. Từ đó suy ra CF vuông góc AB.
c)BE cắt AD tại H. C/m: góc AFH = 90o. Từ dó suy ra ba điểm C,H,F thẳng hàng.
d)C/m: DE = 1/2 BC
#Toán lớp 7
0
TT
Trịnh Tài Đức
19 tháng 4 2016 - olm

Cho tam giác ABC vuông tại A có ABC = 60độ

a) So sánh AB và AC

b) Trên cạnh BC lấy điểm D sao cho BD = AB. Qua D dựng đường vuông góc với BC cắt tia đối AB tại E. C/m tam giác ABC = tam giác DBE

c) Gọi H là giao điểm của ED và AC. C/m tia BH là phân giác của góc ABC

d) Qua B dựng đường vuông góc với AB cắt đường thẳng ED tại K. C/m tam giác HBK đều

 
#Toán lớp 7
2
OB
Oo Bản tình ca ác quỷ oO
19 tháng 4 2016

a) vì tam giác ABC vuông tại A và có góc ABC = 600

=> tam giác ABC đều

=> AB = AC = BC

hihi!!!

Đúng(0)
OB
Oo Bản tình ca ác quỷ oO
19 tháng 4 2016

Trịnh Tài Đức mk giải sai rùi sorry do đọc ko kĩ đề hì !!!!!!

756865

Đúng(0)
LN
Lê Nguyễn Mai Thảo
16 tháng 12 2018 - olm

cho tam giác abc có ab=ac. gọi h là trung điểm của cạnh bc. a) Cm tam giác ABC=tam giác ACH và Ah là tia phân giác góc BAC. b) Vẽ HD vuông góc AC tại D. Trên cạnh AB lấy E sao cho AE=AD. Tính góc AED. c) GỌi M là giao điểm AB và DH. Đường thẳng qua M và song song với ED cắt tia AC tại N. Cm N,H,E thẳng hàng
#Toán lớp 7
0
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP