Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tam giác ABC vuông tại A (gt)
=> góc B + góc C = 90
mà góc B = 60
=> góc C = 30
=> góc C < góc B xét tam giác ABC
=> AB < AC (đl)
tgiac ABC vuông ở , B=60¤=> C=30¤
=>AC>AB vì
AC là cạnh đối diện với góc lớn hơn (60¤)
AB.......................................nhở hơn (30¤)..

b) Xét tam giác abc và tam giác dbe có:
\(\widehat{b}\): góc chung
ab = bd (gt)
\(\widehat{bac}\)= \(\widehat{bde}\)( = 90 độ )
Vậy: tam giác abc = tam giac dbe

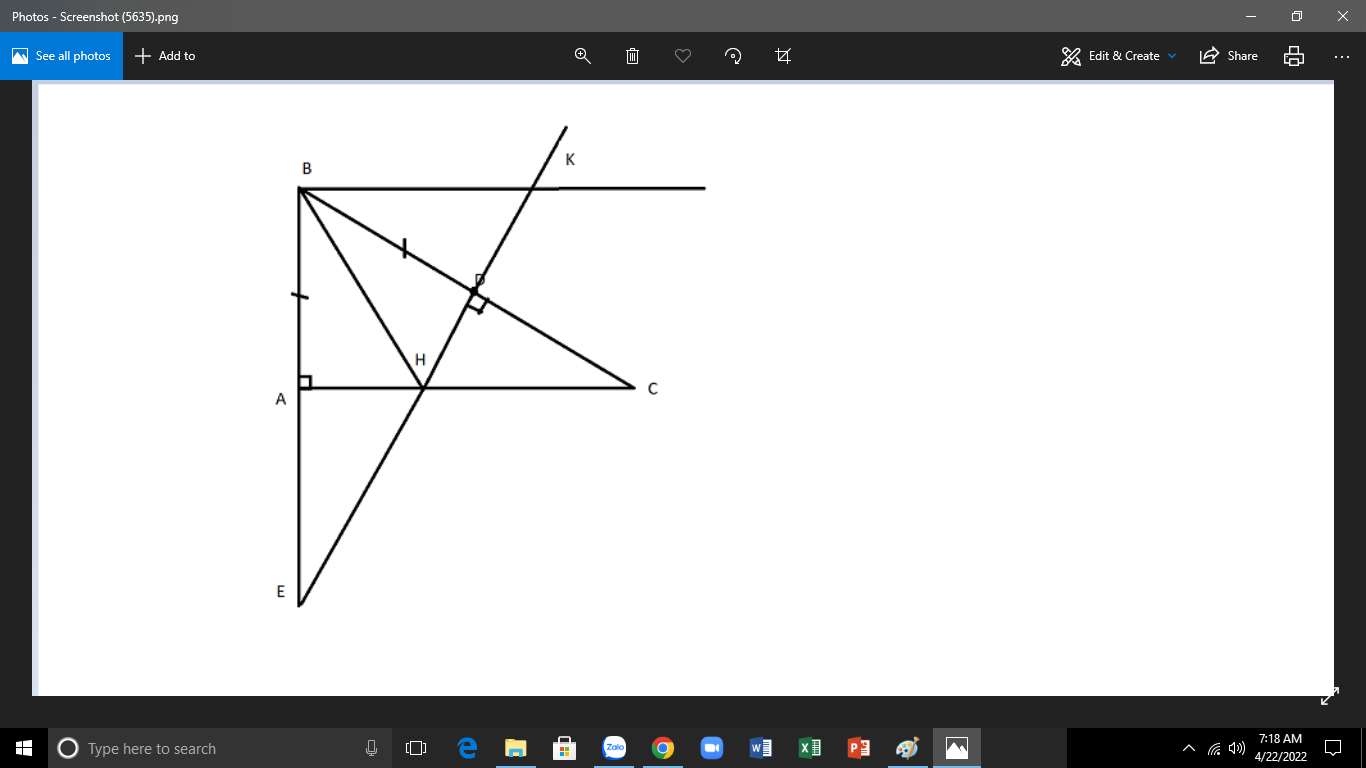
\(\text{a)Xét }\Delta ABC\text{ có:}\)
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\left(\text{tính chất tổng ba góc một tam giác}\right)\)
\(\Rightarrow\widehat{C}=180^0-\left(\widehat{A}+\widehat{B}\right)\)
\(\Rightarrow\widehat{C}=180^0-\left(90^0+60^0\right)=30^0\)
\(\text{Xét }\Delta ABC\text{ có:}\)
\(\widehat{A}>\widehat{B}>\widehat{C}\left(90^0>60^0>30^0\right)\)
\(\Rightarrow BC>AC>AB\left(\text{quan hệ giữa góc và cạnh đối diện trong tam giác}\right)\)
\(\Rightarrow AB< AC\)
\(b)\text{Xét }\Delta ABC\text{ và }\Delta DBE\text{ có:}\)
\(\left\{{}\begin{matrix}\widehat{B}\text{ chung}\\\widehat{BAC}=\widehat{BDE}=90^0\left(gt\right)\\BD=AB\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABC=\Delta DBE\left(g-c-g\right)\)
\(c)\text{Xét }\Delta ABH\text{ và }\Delta DBH\text{ có:}\)
\(\left\{{}\begin{matrix}BD=AB\left(gt\right)\\BH\text{ chung}\\\widehat{BAH}=\widehat{BDH}=90^0\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABH=\Delta DBH\left(ch-gn\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{DBH}\left(\text{hai góc tương ứng}\right)\)
\(\Rightarrow BH\text{ là phân giác }\widehat{ABC}\)
\(d)\text{Mik k bt:< }\)

Goc ABD=58 => DBK=32 => HBK=61 (1)
BHD=180-90-29(58/2)=61 (2)
Tu (1) va (2) suy ra HBK=BHK=61 => tam giac BHK can :)

a) vì tam giác ABC vuông tại A và có góc ABC = 600
=> tam giác ABC đều
=> AB = AC = BC
hihi!!!
Trịnh Tài Đức mk giải sai rùi sorry do đọc ko kĩ đề hì !!!!!!
756865