Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\frac{a}{ab+a+2}+\frac{b}{bc+b+1}+\frac{2c}{ac+2c+2}\)
\(=\frac{a}{ab+a+abc}+\frac{b}{bc+b+1}+\frac{abc^2}{ac+abc^2+abc}\)
\(=\frac{a}{a\left(bc+b+1\right)}+\frac{b}{bc+b+1}+\frac{abc^2}{ac\left(bc+b+1\right)}\)
\(=\frac{1}{bc+b+1}+\frac{b}{bc+b+1}+\frac{bc}{bc+b+1}\)
\(=\frac{bc+b+1}{bc+b+1}=1\)

Đặt B = \(bc\left(y-z\right)^2+ca\left(z-x\right)^2+ab\left(x-y\right)^2\)
\(=bcy^2+bcz^2+caz^2+cax^2+abx^2+aby^2-2\left(bcyz+acxz+abxy\right)\) (1)
Từ \(ax+by+cz=0\Rightarrow\left(ax+by+cz\right)^2=0\)
=>\(a^2x^2+b^2y^2+c^2z^2+2\left(bcyz+acxz+abxy\right)=0\)
=>\(a^2x^2+b^2y^2+c^2z^2=-2\left(bcyz+acxz+abxy\right)\) (2)
Thay (2) vào (1) ta được:
\(B=ax^2\left(b+c\right)+by^2\left(a+c\right)+cz^2\left(a+b\right)+a^2x^2+b^2y^2+c^2z^2\)
\(=ax^2\left(a+b+c\right)+by^2\left(a+b+c\right)+cz^2\left(a+b+c\right)\)
\(=\left(ax^2+by^2+cz^2\right)\left(a+b+c\right)\)
Vậy \(A=\frac{\left(ax^2+by^2+cz^2\right)\left(a+b+c\right)}{ax^2+by^2+cz^2}=a+b+c\)

\(A=\left(x+a\right)\left(x+b\right)\left(x+c\right)\)
\(=\left(x^2+ax+bx+ab\right)\left(x+c\right)\)
\(=x^3+ax^2+bx^2+abx+cx^2+acx+bcx+abc\)
\(=x^3+\left(a+b+c\right)x^2+\left(ab+bc+ca\right)x+abc\)
Theo bài ra ta có:
\(a+b+c=6\)
\(ab+bc+ca=-7\)
\(abc=-60\)
\(\Rightarrow A=x^3+6x^2-7x-60\)
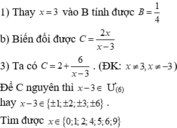
\(A=\left(x+a\right)\left(x+b\right)\left(x+c\right)\\ =\left(x^2+ax+bx+ab\right)\left(x+c\right)\\ =x^3+\left(a+b+c\right)x^2+\left(ab+bc+ca\right)x+abc\\ =x^3+6x^2-7x-60\)
\(B=\left(x+y+z\right)^2=\left[\left(x+y\right)+z\right]^2\\ =\left(x+y\right)^2+2\left(x+y\right)z+z^2\\ =x^2+2xy+y^2+2xz+2yz+z^2\\ =x^2+y^2+z^2+2xy+2yz+2zx\)
Bạn ơi! Ở bài 1 dòng thứ ba tại sao nó lại như vậy:)