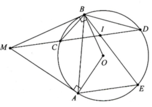
Cho đường tròn tâm O đường kính AB. Trên tiếp tuyến của đường tròn tại A lấy điểm M , từ M kẻ cát tuyến MCD( C nằm giữa M và D; tia MC nằm giữa hai tia MA và MO) và tiếp tuyến thứ hai MI với đường tròn (O) . Đường thẳng BC và BD cắt đường thẳng OM lần lượt tại E và F. Chứng minh rằng O là trung điểm của EF.
(Tt giúp mik cái)-Thank trước


Hok tốt
MO là trung trực của AI => MO vuông góc AI, có BI vuông góc AI => MO || BI
Ta thấy MA.MI là hai tiếp tuyến kẻ từ M đến (O), MCD là cát tuyến của (O), do đó (ICAD)=−1(ICAD)=−1
Vì B nằm trên (O) nên B(ICAD)=−1B(ICAD)=−1, mà MO || BI, MO cắt BC,BA,BD tại E,O,F nên O là trung điểm EF.
Thnk bạn