Vẽ tia phân giác của 1 góc như sau: Đánh dấu 2 cạnh của góc 4 đoạn thẳng bằng nhau OA=AB= OC=CD . Kẻ các đoạn thẳng AD, BC chúng cắt nhau ở K . Hãy giải thích vì sao OK là tia phân giác của góc AOC ? ( nếu có thể nhờ các bạn vẽ hình giúp mình nhé ! )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 6 2017
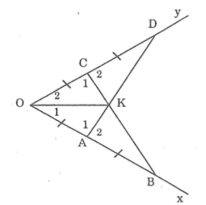
Suy ra: ∠D = ∠B(hai góc tương ứng)
Và ∠C1 =∠A1 (hai góc tương ứng)
Lại có: ∠C1+∠C2 =180°(hai góc kề bù)
Và ∠A1+∠A2=180°(hai góc kề bù)
Suy ra: ∠C2 =∠A2
Xét ΔKCD và ΔKAB, ta có:
∠B = ∠D (chứng minh trên )
CD=AB (gt)
∠C2 =∠A2 (chứng minh trên)
suy ra: ΔKCD= ΔKAB,(g.c.g)
=>KC=KA (hai cạnh tương ứng)
Xét ΔOCK và ΔOAK, ta có:
OC = OA (gt)
OK chung
KC = KA (chứng minh trên)
Suy ra: ΔOCK = ΔOAK (c.c.c)
=> ∠O1=∠O2̂(hai góc tương ứng)
Vậy OK là tia phân giác góc O
CM
2 tháng 12 2018
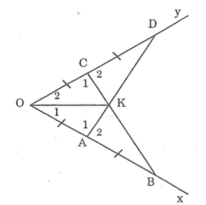
+) Ta có: OC = OA; CD = AB nên:
OC + CD = OA + AB hay OD = OB.
+) Xét ΔOAD và ΔOCB. Ta có:
OA = OC (gt)
∠O chung
OD = OB (chứng minh trên )
Suy ra: ΔOAD= ΔOCB (c.g.c)
17 tháng 5 2017
Vì OA = AB = OC = CD
=> OD = OB
Xét \(\Delta OAD\)và \(\Delta OCB\)có:
OA = OC (gt)
\(\widehat{O}\)(chung)
OD = OB (cmt)
Do đó: \(\Delta OAD=\Delta OCB\) (c-g-c)
=> \(\widehat{ODA}=\widehat{OBC}\) (2 cạnh tương ứng)
=> \(\widehat{OCB}=\widehat{OAD}\) (2 cạnh tương ứng)
Vì \(\widehat{OCB}=\widehat{OAD}\) mà \(\widehat{OCB}+\widehat{DCB}=180^0\)(kề bù)
và \(\widehat{OAD}+\widehat{DAB}=180^0\)(kề bù)
Do đó: \(\widehat{DAB}=\widehat{BCD}\)
Xét \(\Delta KAB\)và \(\Delta KCD\)có:
\(\widehat{ODA}=\widehat{OBC}\)(cmt)
AB = CD (gt)
\(\widehat{CDK}=\widehat{ABK}\left(\widehat{ODA}=\widehat{OBC}\right)\)
Do đó: \(\Delta KAB=\Delta KCD\left(g-c-g\right)\)
=> CK = KA (2 cạnh tương ứng)
Xét \(\Delta OCK\)và\(\Delta OAK\)có:
CK = KA(cmt)
OK (chung)
OA = OC (gt)
Do đó: \(\Delta OCK=\Delta OAK\left(c-c-c\right)\)
=> \(\widehat{COK}=\widehat{AOK}\) ( 2 góc tương ứng )
=> OK là tia phân giác \(\widehat{O}\)
14 tháng 10 2021
Ta có: OA = OC (gt)
⇒ ∆ OAC cân tại O
⇒ˆA1=1800–ˆAOC2⇒A^1=1800–AOC^2 (tính chất tam giác cân) (1)
OB = OD (gt)
⇒ ∆ OBD cân tại O
⇒ˆB1=1800–ˆBOD2⇒B^1=1800–BOD^2 (tính chất tam giác cân) (2)
ˆAOC=ˆBODAOC^=BOD^ (đối đỉnh) (3)
Từ (1), (2) và (3) suy ra: ˆA1=ˆB1A^1=B^1
⇒ AC // BD (vì có cặp góc ở vị trí so le trong bằng nhau)
Suy ra: Tứ giác ACBD là hình thang
Ta có: AB = OA + OB
CD = OC + OD
Mà OA = OC, OB = OD
Suy ra: AB = CD
Vậy hình thang ACBD là hình thang cân.
14 tháng 10 2021
Ta có: OA = OC (gt)
⇒ ∆ OAC cân tại O
⇒ˆA1=1800–ˆAOC2⇒A^1=1800–AOC^2 (tính chất tam giác cân) (1)
OB = OD (gt)
⇒ ∆ OBD cân tại O
⇒ˆB1=1800–ˆBOD2⇒B^1=1800–BOD^2 (tính chất tam giác cân) (2)
ˆAOC=ˆBODAOC^=BOD^ (đối đỉnh) (3)
Từ (1), (2) và (3) suy ra: ˆA1=ˆB1A^1=B^1
⇒ AC // BD (vì có cặp góc ở vị trí so le trong bằng nhau)
Suy ra: Tứ giác ACBD là hình thang
Ta có: AB = OA + OB
CD = OC + OD
Mà OA = OC, OB = OD
Suy ra: AB = CD
Vậy hình thang ACBD là hình thang cân.
14 tháng 11 2016
Bài 2:
Nối C với D ta được đoạn thẳng CD
Nối C với B, B với D, D với A, A với C, A với B ( Nói chung là gần giống vs hình của hoàng thị ngọc anh)
a)Xét tam giác ABC và tam giác ABD có:
AB chung
BC=AC (cùng cung tròn tâm A và B, bán kính AB)(gọi giải thích này là(1))
BD=AD (như trên)
-> 2 tam giác này bằng nhau(2)
b)Xét tam giác ACD và tam giác BCD có:
CD chung
AC=BC (1)
AD=BD (1)
-> 2 tam giác này bằng nhau
c) vì tam giác ABC bằng tam giác ABD (2)
-> góc CAB bằng góc BAD (2 góc tương ứng)
vậy AB là tpg của góc A
14 tháng 11 2016
a) Vì AC thuộc đường tròn (A;AB)
AD thuộc đg tròn (A;AB)
=> AC = AD
Tượng tự: BC thuộc đg tròn (B;AB)
BD thuộc đg tròn (B;AB)
=> BC = BD
Xét tg ABC và tg ABD có:
AC = AD ( c/m trên)
AB cạnh chung( GT)
BC = BD ( c/m trên)
=> ΔABC = ΔABD ( c.c.c)→ ĐPCM
Ttự: AC ϵ (A; AB)
BC ϵ (B; AB). Do 2 đg tròn có bán kính bằng nhau
=> AC = BC
TT: AD = BD
Xét ΔACD và ΔBCD có:
AC = BC (c/m trên)
CD cạnh chung
AD = BD ( c/m trên)
=> ΔACD = ΔBCD(c.c.c)→ ĐPCM
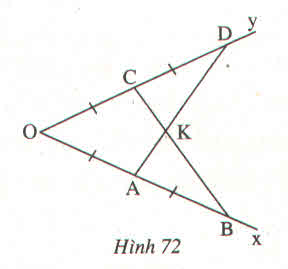
Bạn ơi, phải là Kẻ AD và BC chứ ?
uk , mk nhầm , xin lỗi . Kẻ AD và BC nha mn !!