Cho tam giác ABC.Kẻ BD vuông góc với AC (D thuộc AC).Chứng minh rằng nếu 3.BD bình phương+2.AD bình phương+CD bình phương =AB bình phương +BC bình phương +CA bình phương thì tam giác ABC cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 6 2016
Bạn ơi đề thiếu hay sao ấy
Phải là :
BD2 - CD2 = ?
Sửa đi mik giải cho
21 tháng 8 2021
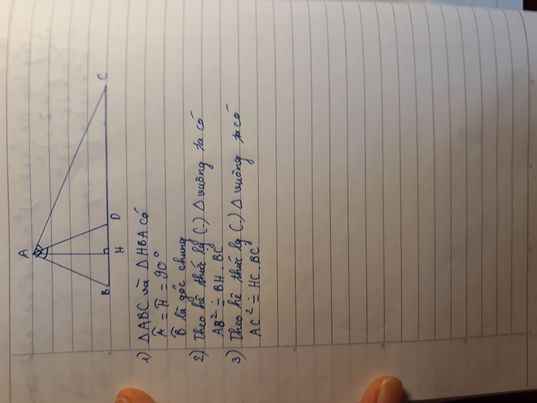
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
2: Ta có: ΔABC\(\sim\)ΔHBA
nên \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
hay \(AB^2=BH\cdot BC\)
3: Xét ΔACH vuông tại H và ΔBCA vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔACH\(\sim\)ΔBCA
Suy ra: \(\dfrac{CA}{CB}=\dfrac{CH}{CA}\)
hay \(CA^2=CH\cdot CB\)
22 tháng 8 2021
1: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔABH\(\sim\)ΔCBA
2: Ta có: ΔABH\(\sim\)ΔCBA
nên \(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)
hay \(BA^2=BH\cdot BC\)
25 tháng 8 2021
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
2: Ta có: ΔABC\(\sim\)ΔHBA
nên \(\dfrac{AB}{HB}=\dfrac{CB}{AB}\)
hay \(AB^2=HB\cdot BC\)
