Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔABH\(\sim\)ΔCBA
2: Ta có: ΔABH\(\sim\)ΔCBA
nên \(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)
hay \(BA^2=BH\cdot BC\)

1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
2: Ta có: ΔABC\(\sim\)ΔHBA
nên \(\dfrac{AB}{HB}=\dfrac{CB}{AB}\)
hay \(AB^2=HB\cdot BC\)

a, Xét ΔABH và ΔAHD có
Góc A chung
Góc ADH=Góc AHB=90°
=> ΔABH ~ΔAHD(g.g)
=> AH/AB=AD/AH
=> AB.AD=AH²(1)
Xét ΔAEH và ΔAHC có:
Góc A chung
Góc AEH = góc AHC
=>ΔAEH~ΔAHC(g.g)
=> AE/AH=AH/AC
=>AE.AC=AH²(2)
Từ (1);(2) => AD.AB=AE.AC(đpcm)
b, vì ΔABC vuông tại A có AI là trung tuyến ứng với cạnh huyền=> BI=IC=AI
=> ΔAIC cân tại I
=>góc IAC =góc ICA
Ta cũng có ΔBIA cân tại I =>góc IBA=góc BAI
Mà góc BAI =góc AED(cùng phụ)
=> góc IBA=góc AED
Mà ABI+góc ACI= 90°
=> gócAED + góc IAC=90°
=> DEvuông góc vs AI
c,
mình làm câu c,d nek bạn
c, ta có\(\Delta\)HEC vuông tại E( vì E là hình chiếu của H nên Góc E=90 độ)
=> EN là đường trung tuyến ứng vs cạnh huyền
=> EN=NH=NC( vì N là trung điểm của HC)
=> \(\Delta\)ENC cân tại N(NE=NC cmt)
=> góc NEC=góc NCE(hai góc đáy) (1)
chứng minh tương tự trong \(\Delta\)BMD cân tại M
=> góc DBM=góc MDB(2)
ta có \(\Delta\)ABC vuông tại A nên góc DBM+góc NCE=90 độ
=>góc MDB+ góc NEC(vì (1);(2)) (3)
và \(\Delta\)\(\Delta\)
DAE vuông tại A nên góc ADE+góc AED=90 độ (4)
từ (3);(4)=>góc BDM+góc ADE=90 độ
=> góc MDH+góc HDE=90 độ ( 180 độ - (MDH+HDE))
=> DM\(\perp\) DE (*)
và góc DEA+ góc NEC=90 độ
=> góc HDE+góc HEN= 90 độ
=> DE\(\perp\) EN (**)
từ (*); (**)=> MDEN là hình thang (DM // EN vì cùng \(\perp\)vs DE)
d, Ta có DHEA là hình chữ nhật (góc D= góc H =Góc E=90 độ)
=> OH=OA=OD=OE (t/c đường chéo hcn)
=> OH=OA=HA/2
ta có HM+HN=BM+NC(vì BM=MH; NH=NC)
=> MH+HN=BC/2=>MN=1/2 BC
diện tích \(\Delta\)ABC =1/2. AH. BC
diện tích \(\Delta\)MON=1/2.OH.MN=1/2.1/2AH.1/2BC
Vậy (S\(\Delta\) MON)/(S\(\Delta\)ABC)=(1/2.AH.BC)/(1/8 AH.BC)
=4
Mình nghĩ là làm như vậy, có gì bạn góp ý nha![]()

a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HD là đường cao ứng với cạnh huyền AB, ta được:
\(AD\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔACH vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b) Xét tứ giác ADHE có
\(\widehat{EAD}=90^0\)
\(\widehat{AEH}=90^0\)
\(\widehat{ADH}=90^0\)
Do đó: ADHE là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Suy ra: AH=DE(hai đường chéo)(3)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)(4)
Từ (3) và (4) suy ra \(DE^2=HB\cdot HC\)

Bạn ơi đề thiếu hay sao ấy
Phải là :
BD2 - CD2 = ?
Sửa đi mik giải cho

Lời giải:
a) Áp dụng hệ thức lượng trong tam giác vuông với:
+) Tam giác $AHB$ vuông tại $H$, đường cao $HD$:
$AD.AB=AH^2(1)$
+) Tam giác $AHC$ vuông tại $H$, đường cao $HK$:
$AK.AC=AH^2(2)$
Từ $(1);(2)\Rightarrow AD.AB=AK.AC$
b) Dễ thấy $ADHK$ là hình chữ nhật do $\widehat{A}=\widehat{D}=\widehat{K}=90^0$
$\Rightarrow AH=DK$
$\Rightarrow 2DK^2=2AH^2(3)$
Từ $(1);(2)\Rightarrow AD.AB+AK.AC=2AH^2(4)$
Từ $(3);(4)\Rightarrow AD.AB+AK.AC=2DK^2$ (đpcm)

a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
XétΔABC vuông tại A có AH là đường cao
nên \(AH*BC=AB*AC\)
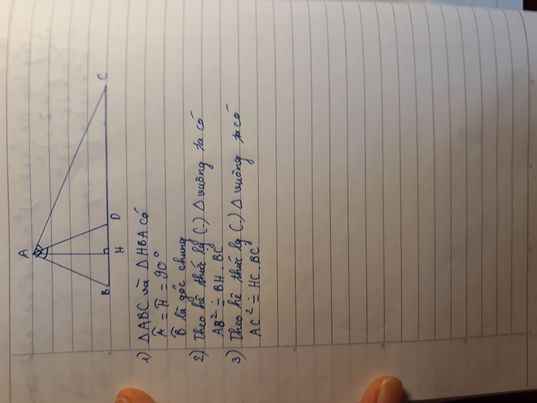
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
2: Ta có: ΔABC\(\sim\)ΔHBA
nên \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
hay \(AB^2=BH\cdot BC\)
3: Xét ΔACH vuông tại H và ΔBCA vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔACH\(\sim\)ΔBCA
Suy ra: \(\dfrac{CA}{CB}=\dfrac{CH}{CA}\)
hay \(CA^2=CH\cdot CB\)